¿Vivimos en un universo de Möbius?: La antimateria somos nosotros

¿Qué es el universo?, ¿por qué existe?, ¿tuvo realmente un principio?

Hola amigos de Tardigrados. Hoy os voy a regalar algunas pinceladas autobiográficas, no exentas de sorna.

Cuando nací, hace ya muchos años, tuve una sensación muy desagradable, y lo recuerdo perfectamente. Alguien me azotó con fuerza, me puse a llorar, abrí los ojos y me vi boca abajo cogido por los pies, con el cordón umbilical ya cortado, y me pregunté que coño era todo esto. Cuando me di cuenta, mi llanto se agudizó con rabia. Me había dado cuenta de que había nacido el universo y de que me esperaba un arduo camino lleno de vicisitudes, hasta llegar a comprender totalmente el sentido que tenía todo esto.

Cuando llegué a los tres años de vida, un día me encontré jugando, en la calle de tierra, con un juguete de madera que mi padre había fabricado para mí. En un descuido, cuando me aburrí del juguete, alguien me lo robó. Mi madre me preguntó dónde estaba el juguete, qué había hecho con él, pero no supe qué responder. Me quedé un rato más sentado en la calle de tierra, miré hacia el final de la calle y vi al hijo del vecino jugando en la puerta de su casa con mi juguete, que ahora era suyo, porque mi juguete al ser abandonado por mi, tuvo la suerte de conseguir ser adoptado por un nuevo dueño. Nunca lo recuperé, ni supe más de él. Pero, aquel mismo día tuve un pensamiento lleno de lucidez en el mismo sitio donde me robaron el juguete. Ese pensamiento tan lúcido era el siguiente: “todo lo que existe, (que ahora llamamos universo) nunca tuvo un principio y nunca tendrá un final. Y esa es la razón más simple que explica todo lo complejo. Algo que es eterno no tiene necesidad de ser creado“.

Amigo lector, te estarás preguntado, cómo es posible que a mi corta edad, yo pueda haberme preguntado esas cosas tan profundas o incluso recordar el momento de mi nacimiento. El momento de nuestro nacimiento constituye un cambio de medio muy brusco. Es como darse un chapuzón en agua helada, el auténtico bautismo. A esa sensación, tarde o temprano la vistes con elementos reconocibles para poder ser recordaba. En cambio, el pensamiento cosmogónico que elaboré a los tres años de edad, no es la típica clase de pensamientos que se suelen tener los niños de esa edad, lo reconozco. También puede ser que todo haya sido un cúmulo de falsos recuerdos, y yo esté alucinando con ellos, creyendo que fueron reales alguna vez en mi experiencia vital.

Nacimiento del Universo

Siguiendo este razonamiento cosmogónico, podemos afirmar que todo lo que existe en el universo, no es que esté conectado de alguna manera, sino que es la misma cosa, aunque observada parcialmente y desde puntos de vista diversos. Por lo tanto, no es extraño, que lo que en física cuántica se llama “entrelazamiento cuántico“, sea en realidad, no entrelazamiento, sino la constatación de que todo en este universo es parte de todo. Nada está conectado, porque el concepto de conexión implica la existencia previa de entidades separadas, aisladas. El nexo universal, es pues la interconexión necesaria de algo que nunca estuvo separado, sino que cualquier parte es necesariamente coherente con todas las demás.

¿Por qué existe el universo?. Existe una corriente de consenso oficial, que yo suelo llamar sarcásticamente “mainstreamófila“, en la cual algunos de sus gurús exponen con orgullo preguntas estúpidas a cerca del universo, como por ejemplo esta: ¿”Por qué hay algo donde no debería haber nada“?. Es más que evidente que toda pregunta estúpida tiene la interesante propiedad de contestarse a sí misma. “Mire usted, hay algo, porque si no hubiera nada, nadie tendría la posibilidad de hacerse esa pregunta estúpida, ¿ok, tonto del culo?“. Preguntas de este estilo se las he oído a muchos “gurús“, que van por ahí dando charlas, y participando en debates, entrevistas, etc, y cobrando dinero por todo ello, y haciéndose los interesantes y super-inteligentes gallitos que todo lo saben. Uno de esos gallitos, es Bryan Greene, y en youtube puedes encontrar miles de videos, como este que pongo de muestra,

mostrando lo super-inteligentes que son todos estos “gurús” del “universo de pacotilla” que nos explican. La lista de estos gurús mainstreamófilos, que están ahí para darnos lecciones a todos, se extiende casi hasta el infinito. Además de Bryan Green, están Sean Carroll, Max Tegmark, y miles más.

Básicamente, todos son “influencers” de la corriente yanqui de la posverdad, donde el multiverso, la teoría de cuerdas, la supersimetría, y las ondas gravitacionales son algunos de sus pilares de sustentación, de sus carteras repletas de billetes, por adoctrinar a las masas con sus mierdas. He elegido ese video de youtube, al azar. Entras en youtube, escribes en la barra de búsquedas el nombre de algunos de estos gurús y te salen miles de videos encontrados, todos hablando de la misma mierda ( el Big Bang, las materia oscura, la energía oscura, los agujeros, negros, el multiverso, las ondas gravitacionales, etc, etc, etc). Y lo más gracioso de todo es que te lo venden como si fuera la Verdad Absoluta e Indiscutible. Respecto a la inflación cosmica, lo único que está inflado realmente es el ego de todos estos gurús, y sus respectivas billeteras.

Transcribramos y analicemos brevemente ese video que he puesto de muestra, de todos estos “gurús tan geniales“:

“La ultima pregunta”: ¿Por qué hay algo en lugar de nada”. Por todos los países esta cuestión ha desconcertado e intrigado a muchos filósofos, científicos y teólogos. Si resulta que es un universo eterno, o es una deidad eterna, parece que nadie ha podido responder con coherencia por qué eso debe ser así, en un sentido u otro. Sin embargo, hay al menos algo que sí podemos saber, algo que tiene una existencia innata, algo que se deja capturar racionalmente.

– Max Tegmark: Por su puesto, si dices que existimos porque algo nos creó, y que antes otra causa creó a esa, etc. Entonces, siempre estarás buscando la siguiente causa que creó la causa anterior, nunca acabarás de buscar. Pero, yo creo que hay una especie de objeto real ahí afuera que fue claramente no creado. Y hay objetos matemáticos, como el cubo, por ejemplo, y no estoy hablando de cubos como terrones de azúcar, o que sea una especie de combustible físico, sino de un objeto matemático, conocido por los matemáticos como el cubo sobre un dodecahedro, sobre una esfera, o un espacio vectorial. Todos estos objetos existen, independientemente del espacio y el tiempo, existen claramente fuera de ese universo espacio-temporal. Ese cubo no fue creado hace 14 millones de años en el Big Bang, ¿verdad?. Y sin embargo, ves que ese objeto ya existe ahí, inmutable, perfecto siempre. Existe, y tienes la impresión de que ese objeto ya existía antes de que pensáramos en él, que nosotros no hemos inventado ese cubo. La idea de que ese objeto es un cubo no es una idea arbitraria, una idea que pueda ser inventada.

Esto explica por qué los objetos matemáticos existen, pero ¿por qué existen los planetas, las mentes, las rocas?

– Bryan Greene: El multiverso simulado, aunque viene con mucho razonamiento directo en la matriz cuyos cerebros están siendo estimulados para pensar que están en una determinada realidad, aunque no lo estén, sino que son entidades simplemente instaladas en receptáculos de hardware, conectadas a un computador central. Ese podría ser el caso. La razón por la que yo hablo de esta idea en mi libro, no es porque me la tome en serio. Pero hay una conclusión interesante: que esta clase de razonamiento te permite hacerte la siguiente: pregunta ¿son las matemáticas una descripción de la realidad, o son por sí mismas la misma realidad?. ¿Son las matemáticas algo inventado, o es algo descubierto, algo que ya estaba ahí antes de que se nos ocurriera pensar en ello? ¿Son algo preexistente que ya formaba parte del tejido del tapiz que es la realidad?. El multiverso simulado del que hablo en mi libro, te da la posibilidad de hacerte es pregunta. Porque si tu y yo, formamos parte ahora mismo de la misma simulación informática. Eso esta muy bien, siento que es real para mí, y es un buen disfraz con el que la realidad nos quiere hacer creer que no estamos en ninguna simulación informática. Pero, imagina que abrimos ese computador donde se está ejecutando la simulación, y miramos lo que hay dentro, ¿qué veremos?. Lo que veríamos sería algo muy parecido a infinidad de ceros y unos siendo manipulados mediante infinidad de ecuaciones matemáticas. Por lo tanto, si eso es lo que somos, entonces, seríamos sólo matemáticas. Seriamos solo el despliegue, el resultado de aplicar ecuaciones matemáticas sobre objetos matemáticos, para transformarlos o crear otros nuevos. Y eso significaría que las matemáticas serían la misma realidad, la realidad misma.

– Max Tegmark: Una de las cosas mas interesantes que hemos descubierto, a lo largo de los siglos, es que las matemáticas están por todas partes. Ya Galileo nos explicaba que la naturaleza, el libro de la naturaleza, está escrito en el lenguaje de las matemáticas, y después de que él hiciera esa observación, la gente fue descubriendo más y más regularidades, más simetrías, maravillosas relaciones matemáticas. Descubrieron y se sorprendieron de ver cómo con las matemáticas se podía modelar tan bien la realidad. Después se descubrió el Modelo Estándar de la Física de Partículas, Y la razón por la que yo creo que la naturaleza puede ser descrita tan bien mediante las matemáticas es que, en una ultima y muy profunda instancia, la naturaleza son matemáticas.

Y ahí está la respuesta a tu pregunta.

No, ni la naturaleza es en sí misma matemáticas, ni estamos en una simulación informática. Por mucho que se empeñen Bryan Green, Max Tegmark, y muchos otros gurús de la posverdad, en adoctrinarnos con sus ideas, nuestro universo, es real, no es una simulación, y tampoco está hecho de matemáticas. Si el universo fuera matemáticas, entonces sí habrían muchas probabilidades de que todo fuera una simulación informática. La prueba de que nuestro universo no es matemáticas está en que hay cosas que las matemáticas no puede modelar. Por ejemplo, la emergencia de la consciencia humana, no puede ser simulada desde procesos y estructuras matemáticas.

La mente humana nunca podrá comprenderse totalmente a sí misma, siempre quedarán recintos psíquicos inaccesibles. Pero, no hace falta ejemplos tan rebuscados para darse cuenta que las matemáticas no pueden modelar perfectamente la naturaleza, y menos identificarse con ella. El ejemplo más simple que se me ocurre es la suma 1 + 1 = 2. En esa sencilla ecuación hay un ejemplo perfecto de pérdida de información. Si nos dan el resultado, 2, y nos piden que hallemos los números desde los que alguien realizó la suma, nunca podremos saber qué sumandos fueron utilizados. Esa información se pierde de forma irreversible cuando se realiza la suma. Luego, las matemáticas no tienen memoria. Si la naturaleza fuera sólo matemáticas, sería un ente sin memoria. Supongamos, ahora, que la naturaleza, el universo, fuera el continuo resultado de una simulación informática ejecutándose en una especie de super-ordenador. Lo más parecido a eso que podemos imaginar sería un fractal infinito, como el que realicé hace ya algunos años con el titulo de “fragmento de Arrenia II”

Yo poseo todo el código fuente, y todas las ecuaciones matemáticas necesarias para generar esa clase de fractales infinitos. Navegar por un mundo infinito de esas características, un mundo sin bordes, es muy aburrido. Cualquier parte se parece a cualquier otra, nada es especialmente interesante, todo aparece básicamente inerte y estático. La tercera dimensión se confunde con la cuarta, es decir, con la escala. Los colores son falsos. En un fractal solo existe la información de qué puntos pertenecen al conjunto y cuales no. Un punto está dentro o fuera del conjunto que caracteriza al fractal si cumple una serie de propiedades al ser evaluado desde una ecuación matemática. El fractal infinito Arrenia II podría perfeccionarse, y conseguir que aparecieran estructuras dinámicas, transformándose, naciendo unas de otras, incluso se podría conseguir que el observador que lo navegue sienta las texturas, la dureza o blandura, de las superficies de ciertas estructuras, o si están más calientes o frías que su tacto. Incluso podríamos conseguir introducir leyes físicas como la de la gravedad. Pero, Arrenia II seguiría siendo un fractal, infinito, pero fractal. Eso sí, sería más interesante de navegar ahora que antes, porque podrían existir zonas sorprendentes dispuestas a ser descubiertas, muy distintas a las zonas más comunes. Incluso podrían existir zonas que quedarían inaccesibles, eterna o temporalmente, para cualquier navegante-observador. ¿Cual es el problema con Arrenia II y con todo fractal infinito que intente ser una simulación de la realidad?. El problema esencial es ontológico. ¿Qué ocurre si un navegante-observador de esa simulación se encuentra con otro navegador-observador?. ¿puede eso ocurrir?. Y en el caso de que si pudiera ocurrir, ¿podrían interactuar?.

La prueba de que nuestro universo no es una simulación informática, ni nada parecido, es que los navegantes-observadores pueden encontrarse realmente e interactuar. Seres con su propia conciencia, seres inteligentes que te observan, mientras tú les observas a ellos, que te saludan, que te hablan. En una simulación, sólo navega-observa el que está fuera de la simulación. nunca quien está dentro de ella. No se puede nadar y guardar la ropa al mismo tiempo.

Saludos

Negacionismo del Big Bang, ¿qué es el tiempo?, elongación espacio temporal o mengua matérica universal

Dicen que nuestro universo se expande. Peor aún, dicen que se expande aceleradamente, y nos muestran las evidencias. A menudo, en física y otras disciplinas, no sólo científicas, las evidencias son sólo interpretaciones o medias verdades. ¿Hacia dónde se expande nuestro universo?. Como la respuesta a eso es simplemente “hacia ningún sitio”, y como pretenden mantener como cierta la afirmación de que el universo se expande aceleradamente, sólo les queda argumentar que lo que se expande realmente es el espacio-tiempo, por lo que la materia que se encuentra enclavada en él formando cúmulos está en proceso de recesión relativa. Por lo tanto, la elongación espacio-temporal parece ser un hecho irrefutable, pero no, no es irrefutable. Ese supuesto hecho se basa en el desplazamiento hacia el rojo de las rayas espectrales de la luz de galaxias y cúmulos de galaxias que nos está llegando. Ese desplazamiento al rojo se interpreta como si fuera un efecto Doppler, y por lo tanto, se interpreta que existe una velocidad de recesión de cada galaxia que es aproximada y directamente proporcional a la distancia. Pero a mi me surgen muchas dudas sobre todas esas afirmaciones. La primera es si es cierto que el espacio-tiempo se expande y de forma acelerada ¿por qué han de separarse unas de otras las partículas materiales?. O dicho de otra forma. ¿Dónde y qué clase de ancla tiene cada partícula material clavada en ese espacio-tiempo para que sea arrastrada con su expansión?. Alguien puede argumentar con el ejemplo de un gas dentro de un recipiente. Si el recipiente se expande el gas se expande con él, enfriándose y disminuyendo su presión. Pero yo puedo argumentar también que ese gas se expande acompañando al recipiente porque las partículas de ese gas impactan y rebotan continuamente en las paredes del recipiente. Las partículas del gas intercambian calor continuamente con las paredes del recipiente. Pero, ¿dónde están las paredes de nuestro universo?, o peor aún, ¿alguien ha visto alguna vez que las galaxias reboten contra unas supuestas paredes universales?. Nuestro universo no posee bordes materiales, fronteras, barreras sobre las que impactar, colisionar. Parece ser un universo infinito espacial y temporalmente, por lo tanto, cualquier supuesta expansión del espacio-tiempo no arrastraría materia, no puede haber anclaje de la materia en el espacio-tiempo. Cuando matemáticamente sumas a infinito cualquier número real, sigue dando infinito.

Esta reflexión nos lleva inexorablemente a la pregunta: ¿qué es el tiempo?. El tiempo es simplemente el método que utiliza nuestro cerebro para ordenar nuestras experiencias en la memoria. El tiempo es la acción de un librero numerando las páginas del libro de nuestra vida. Objetivamente, el tiempo no existe. En la naturaleza sólo hay presente, y no hay ni futuro ni pasado. Por esa razón los viajes en el tiempo (como los de las pelis de ciencia-ficción) son realmente imposibles. No se puede viajar a un tiempo futuro por la sencilla razón de que no se puede viajar hacia algo que aún no existe. Igualmente, no se puede viajar a un tiempo pasado por la sencilla razón de que ese tiempo pasado no existe. Evidentemente si pudieras viajar a un tiempo pasado te encontrarías con una duplicación de materia, salida de la nada. Pero no hay atajos ni caminos por los que pueda transcurrir la materia hacia tiempos pasados o futuros. Cuando los físicos teóricos actuales entiendan mejor qué es el tiempo y por qué el tiempo no es sólo esa cosa que miden los relojes, estarán en mejores condiciones de elaborar teorías más certeras sobre la naturaleza. Otra característica que define al tiempo es su inexorabilidad: dime cualquier fecha en el pasado y siempre es imaginable saber que esa fecha ocurrió realmente. Dime cualquier fecha en el futuro y te puedo asegurar que esa fecha llegará. Es como el juego de escribir un número real, siempre podemos escribir otro número real mayor o menor que ese. O al escribir dos números reales, siempre podemos encontrar otro distinto entre ambos. Por lo tanto, el tiempo es cuantificable, y para ello usamos los relojes.

Respecto a la pregunta ¿qué es el espacio?, cabe responder de una forma muy análoga a como lo hemos hecho con el tiempo. Pero el espacio no se nos presenta como el tiempo. Nuestros cerebros no ven al espacio como algo que transcurre, sino literalmenete como un recipiente donde están las cosas que percibimos. El tiempo pasa (siempre hay tiempo pasando, nunca se acaba), el espacio permanece. Percibimos el tiempo como algo dinámico y al espacio como algo estático. Pero ambas cosas son productos imprescindibles para ordenar nuestra experiencia.

¿Por qué percibimos el espacio como poseyendo tres dimensiones?. Cuando algunos físicos teóricos nos hablan de otras dimensiones espaciales extra, además de las tres clásicas (ancho, alto y profundo), para esconder su falta de evidencia científica, nos cuentan que esas dimensiones están como enrolladas sobre sí mismas, plegadas microscópicamente y por eso no podemos verlas. Todos sabíamos desde el principio, porque lo aprendimos bien, que lo que caracteriza a un sistema espacial de referencia es la ortogonalidad de sus ejes. Si una dimensión está plegada, retorcida microscópicamente, creo yo que no es una buena opción para un sistema espacial de referencia, porque ese “enrollamiento” no es precisamente la mejor definición de ortogonalidad. Evidentemente, nuestro espacio puede ser descrito matemáticamente mediante muchos ejes (no sólo tres) que no sean ortogonales, pero todos pueden ser reducidos a tres ejes ortogonales desde los que nuestras ecuaciones se simplifican drásticamente para describir lo mismo con igual éxito. El espacio que percibimos posee infinitas direcciones desde las que nos puede llegar el peligro o la salvación. Son infinitas direcciones por las que podemos huir del peligro, o estar alerta, por las que nos puede llegar el depredador a cazarnos. Nuestras tres dimensiones espaciales tienen mucho más que ver con las características de nuestro cerebro (de nuestra mente), que de algo externo. Nuestros antecesores, simios arborícolas, vivían casi todo el día encaramados a sus ramas, y el alimento lo conseguían desplazándose de rama en rama, al mismo tiempo que miraban en todas direcciones para estar alerta de los acechadores. Nuestro sentido de la vista es capaz de percibir con tres colores básicos de los que se derivan todos los demás. Eso es así por evolución natural. Nuestros parientes ancestrales necesitaban distinguir qué fruta estaba madura por su color, qué alimento era aparentemente comestible por su color y cual no. Del mismo modo que nuestro cerebro y nuestros órganos sensoriales han evolucionado para percibir todos los colores de las cosas que pueden ser expresados mediante esos tres colores básicos, una evolución similar se ha producido para percibir lo que llamamos el espacio. Al igual que los tres colores básicos desde los que podemos percibir cualquier otro color, nuestro cerebro percibe el espacio desde tres direcciones básicas, y cualquier otra dirección puede ser expresada mediante ellas. Así pues, cuando nos preguntamos por qué tres dimensiones espaciales, hay que preguntarse por qué tres colores básicos, y la respuesta es más de fisiología humana que de física universal.

El llamado espacio-tiempo, es pues un constructo, algo más teórico que real. Nuestro cerebro casa muy mal el espacio y el tiempo como un espacio de cuadro dimensiones. Nuestro cerebro no admite como muy natural que el tiempo sea un eje más como los otros tres ejes espaciales. Notamos muy bien qué es intuitivamente el tiempo, y por qué no puede ser una dimensión espacial más. La flecha del tiempo es algo muy subjetivo. El futuro es algo que aún no existe y por lo tanto no puede ser apuntado por ninguna fecha con certeza. El pasado es algo que ya no existe, y por lo tanto ninguna flecha pudo apuntar con certeza hacia nuestro presente.

Y por ultimo. ¿Qué hacemos con el Big Bang?. Puesto que toda la evidencia nos viene de supuestos desplazamientos al rojo de lineas espectrales, y que los santones del paradigma cosmológico actual se han encargado de darnos de comer ese fenómeno como si fuera un efecto Doppler cosmológico, lo que tenemos es un universo en creciente estampida. Pero si pensamos un poquito vemos, que ese efecto Doppler, que también se da en las diferencias de potencial gravitatorio, es simplemente algo relativo, de perspectiva, de horizonte, más que ningún supuesto Big Bang. La distancia a escala cosmológica produce sencillamente una diferencia de potencial gravitatorio, pero esa diferencia de potencial no significa ninguna expansión ni ningún alejamiento de las galaxias. Toda la materia permanecería esencialmente estática en nuestro universo, y lo único que cabría explicar es ¿por qué la distancia cosmológica produce diferencias relativas de potencial gravitatorio?. Cuando dibujamos la gráfica de un potencial gravitatorio producido por una masa puntal, lo solemos hacer como una curva en forma de campana invertida cuyos bordes se aproximan infinitamente hacia un eje horizontal, el cual marca un potencial nulo (potencial cero). Es decir, ese potencial es una curva gaussiana invertida, que posee valores negativos, y que se hacen menos negativos a medida que se aproximan al eje horizontal de potencial cero. Pero a escala cosmológica, esa linea de potencial cero podría ser más un arco de circunferencia que una recta real, por lo que además de las diferencias locales de potencial debido a la presencia cercana de materia, existirían diferencias relativas de potencial gravitatorio debido a la distancia.

Supongamos que un Radio de Hubble, es la mayor distancia cosmológica de la que nos puede llegar luz. Existe pues un horizonte cósmico, que podemos cuantificar de la siguiente forma: Supongamos que el potencial cosmológico es la superficie lisa de una esfera, y que los potenciales gravitatorios locales son pequeños montículos que destacan sobre esa superficie. Cuando nos situamos en un montículo se crea un horizonte desde el cual podemos percibir luz procedente de puntos de otros montículos. Si nos situamos en un punto de la superficie el radio de nuestro horizonte se reduce, y solo podremos ver luz procedente de montículos muy promimentes y cercanos. Pero, si nos situamos en una montaña de potencial local muy grande, nuestro horizonte para ver luz será muy grande. Esto resuelve la Paradoja de Olbers. En otras palabras, vemos el número de estrellas y galaxias que vemos por nuestra posición peculiar dentro de nuestra galaxia. Si estuvíéramos en una región remota, muy alejada de cúmulos grandes de materia, como son las galaxias, es decir, en una región muy cercana al potencial cero, veríamos muy pocas estrellas y galaxias en el cielo, menos de las que somos capaces de ver, porque nuestro horizonte observacional sería mas reducido.

Esto significaría que cuanto más cercanos estamos de una gran masa nuestro horizonte cósmico (observacional) será mas grande. Así, nuestra distancia al nuestro horizonte será:

(1)

donde R el radio de Hubble, h nuestra altura local de potencial gravitatorio, s la distancia real al punto H, d la distancia tangencial que recorre la luz.

Figura 1

Esto significa que, según esta teoría del potencial cosmológico, que me estoy inventando, no sólo existe por la misma linea de vision el punto H del horizonte, sino otros más remotos, H1, H2, etc, si están situados sobre potenciales gravitatorios de cierta altura.

Luego en una esfera universal, sin defectos topológicos (como los campos gravitatorios locales), el potencial de deriva cósmica vendrá expresado por la ecuación:

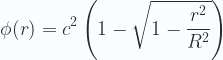(2)

cuya gráfica es la siguiente:

Obviamente, si r es muy pequeña respecto a R, ese potencial de deriva cósmica se reduce a cero. Y cuando r tiende a R, el potencial f tiende a c². En un campo de potencial gravitatorio local, los valores son escalares negativos que crecen con la distancia hacia cero. Pero, en el campo de potencial de deriva cósmica los valores escalares son positivos y tienden con la distancia r hacia el cuadrado de la velocidad de la luz en el vacío.

Desde esa expresión explicita de potencial de deriva cósmica es fácil descubrir que el desplazamiento al rojo de las rayas espectrales de la luz de galaxias remotas es el siguiente:

(3)

donde ? es la longitud de onda original (emitida), y ?? es la diferencia entre la longitud de onda observada y la emitida. Y si queremos expresar la distancia r en función del desplazamiento al rojo z y del radio de Hubble, tendremos:

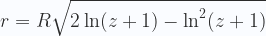(4)

Esto cambia drásticamente las distancias estándar calculadas hasta ahora para las galaxias y cúmulos remotos. Por ejemplo, se ha observado que los desplazamientos al rojo más grandes corresponden a unos extraños objetos remotos que se llaman cuásares. Estos extraños objetos nos ofrecen desplazamientos al rojo que van de z = 0.16 hasta z = 3.53. Lo cual, según mi hipótesis, implica distancias entre r = 0.524R y r = 0.875R.

Mi hipótesis tiene una serie de ventajas frente a las teorías del Modelo Cosmológico Estándar. En mi hipótesis:

1. No existe recesión de galaxias y demás objetos remotos, sino que permanecen esencialmente en reposo. Ese desplazamiento al rojo se debe casi en su mayoría a la diferencia de potencial de la deriva cósmica. Después hay que sumar o restar otros efectos Doppler, debidos a potenciales gravitatorios locales, y/o a velocidades cinemáticas.
2. La localización de la fuente emisora y la del observador en sus respectivos potenciales gravitatorios locales contribuyen al efecto de desplazamiento al rojo, ya que hay que calcular sobre la diferencia neta de potencial (sumando y/o restando potenciales locales y cinemáticos al potencial cosmológico).
3. La Radiación de fondo de Microondas sería según mi hipótesis vulgares fotones emitidos mayoritariamente por átomos de hidrógeno procedentes de galaxias y cúmulos en el horizonte H, incluso más allá de él, en una franja cercana. Es decir de puntos H1, H2, etc, tal como los he dibujado en la figura 1.
4. Los cuásares serían, ni más ni menos que galaxias y cúmulos con alta acumulación de materia y muy cercanos al horizonte cósmico H, pero dentro (no fuera) de la esfera de Hubble.

Por lo tanto, según mi hipótesis cosmológica, nuestro universo observable sería tan sólo un hemisferio de la gran esfera cósmica, esfera universal (no confundir con la esfera de Hubble), que tendría cuatro dimensiones espaciales. El otro hemisferio quedaría inaccesible, en su mayor parte, a nuestra observación de ondas electromagnéticas. Esa cuarta dimensión espacial es sobre la que se curva la linea de potencial cero. Es decir, nuestro universo (el observable y el no observable) sería simplemente la superficie de una hiperesfera de cuatro dimensiones espaciales.

Figura 2 (Esfera universal)

Si queremos traducir los potenciales a velocidades de recesión o viceversa debemos establecer la siguiente equivalencia, la cual es posible porque se usan coordenadas cosmológicas:

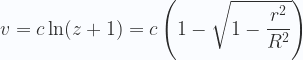(5)

Por ejemplo. Se observó que la galaxia 8C1435+635 posee un corrrimento al rojo de z = 4.25, que es el más grande que se ha conseguido ver hasta ahora. Así desde el Modelo Estándar, ese desplazamiento correspondería a una velocidad de recesión de v = 0.93c. Pero, si usamos las coordenadas cosmológicas tenemos una velocidad de recesión de:

(6)

es decir, una velocidad superlumínica. Y en terminos de diferencia de potencial cosmológico tendriamos:

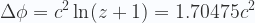(7)

Por lo que esta lejana galaxia estaría algo más allá de nuestro horizonte cósmico. Pero nuestros telescopios la pueden ver porque es una gran acumulación de materia, ya que su altura de potencial gravitatorio sobresaldría un poco por encima de nuestro horizonte cósmico. Toda galaxia o cúmulo más allá de nuestro horizonte que no posea suficiente altura de potencial para destacar, sino que estuviera a ras de él. solo puede ser vista como formando parte de la Radiacíón Cósmica de Fondo. Esto significa que cuando una fuente emisora de luz cercana al horizonte posee poca altura de potencial, no sólo su luz nos llegaría con desplazamiento al rojo, sino con poca intensidad (pocos fotones), y cuanto más grande sea su potencial gravitatorio local más intensa veremos su luz y bien diferenciada del ruido de fondo cósmico.

Saludos

Un universo eterno y transfinito: una foliación conforme del espaciotiempo

Foliación transfinita de la conciencia de Ridley

Nuestro universo podría poseer la forma de una hiperesfera transfinita. Para ver esto fijémonos en lo siguiente (que ya traté en un post anterior). La serie infinita N = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + … es divergente ya que su suma es N = ∞. Pero, puede ser regularizada, como demuestro en el link anterior, para dar una suma de N = -1/2. Es decir, la función Zeta de Riemann toma el valor -1/2 cuando la variable es cero:

Esta suma nos sugiere que el infinito matemático, ∞, en la recta real, coincide con el número real negativo -1/2, y -∞ coincidiría simétricamente con 1/2. Si partimos de un sistema de referencia cartesiano de dos dimensiones, tendremos que los dos ejes ortogonales podrían ser recorridos, partiendo desde el origen de coordenadas, en dos posible direcciones. Para el eje de abscisas, podríamos alcanzar el infinito, por el camino largo (hacia la derecha) hasta llegar al punto (-1/2, 0). O también podríamos alcanzar dicho punto, que representa al infinito, por el camino más corto (andando hacia la izquierda). Sin embargo, si andamos en dirección derecha, desde el origen o cualquier punto de abscisa positiva, (x,0), no podríamos llegar a los puntos situados entre el punto (-1/2, 0) y el (x,0) ya que el infinito actuaria como barrera infranqueable para seguir el camino y cerrar el círculo.

Saludos transfinitos a todos

El mito de la expansión del universo: la anisotropía Doppler demuestra que la Teoria del Big Bang es un camelo, una pura patraña

Queridos y amables lectores de Tardígrados, hace tiempo que vengo reflexionando sobre el origen del universo, sopesando los datos científicos experimentales, y he llegado a una conclusión:

“Nuestro universo nunca tuvo un origen, ni de espacio ni de tiempo. Nuestro universo es estático, infinito en espacio y tiempo, nunca tuvo un principio, y nunca tendrá un final, y permanecerá eternamente idéntico a sí mismo”

Llegué a esta conclusión después de examinar minuciosamente el efecto Doppler que Hubble descubrió en galaxías y cúmulos galácticos distantes. Incluso el mismo Edwin Hubble siempre tuvo la duda de si atribuir ese efecto Doppler a un movimiento de alejamiento (recesión) o a otra causa, el tipo era un científico serio y el método científico le impedía afirmar rotundamente que el corrimiento al rojo de la luz de esas galaxias se debía sin duda a una velocidad cinemática de recesión. Pero, si no es un movimiento de recesión el que causa ese corrimiento hacia el rojo de la luz, ¿qué es?. La clave está en el modelo matemático que usemos para describir ese efecto Doppler. Hace ya mucho tiempo que descubrí que el mejor modelo matemático para describir el efecto Doppler, porque es autosimilar, es el siguiente:

	(1)
	(2)

donde obviamente, f es la frecuencia de la luz medida por el observador, f₀ es la frecuencia original emitida por la fuente de luz, v es la velocidad relativa entre fuente y observador, y c es una constante (299792458 m/s) que muchos dicen que es la velocidad de la luz en el vacío (yo no me atrevería a decir tanto). λ es la longitud de onda medida, y λ₀ es la longitud de onda original.

Hay que advertir también que, la ley de Hubble, se ha convertido en una herramienta estándar para el cálculo de distancias de objetos distantes como galaxias, cúmulos galácticos o quasares. Tan es así que ya nadie discute si un corrimiento al rojo concreto corresponde a cierta distancia astronómica, lo dan por hecho. Es algo muy parecido a la famosa conjetura de Riemann respecto a los ceros de la función Zeta (se da por cierta la conjetura para extraer de ella teoremas a cerca de los números primos). La ley de Hubble, la cual relaciona (o mejor decir que correlaciona) la distancia r con la supuesta velocidad de recesión v, resulta en una ecuación lineal de la siguiente forma

donde la constante R₀ se llama radio de Hubble, como no podía ser de otra forma.

Pero, pensemos un poquito. Seamos un poco escépticos y no nos creamos a pies juntillas que esa correlación lineal de que nos habla la ley de Hubble sea la verdad absoluta de la que no quepa ni siquiera dudar en ningún caso. Pensemos que nuestro universo (al menos nuestro universo observable) es básicamente estático y homogéneo, y que las galaxias y cúmulos de ellas se mueven con distintas velocidades relativas unas de otras, como las partículas de un gas. Pensemos, sólo por un momento, que nuestro universo (observable) no se está expandiendo y por lo tanto una supuesta expansión acelerada sería aún más impensable. Entonces al aplicar nuestra fórmula de doppler (1), observamos algo inédito: galaxias que en principio hemos dicho que se mueven con velocidades aleatorias, ahora resulta que los corrimientos al rojo son más pronunciados que los corrimientos al azul. Efectivamente, nuestra fórmula (1) produce, para un mismo valor absoluto de v, un mayor desplazamiento de la frecuencia. ¿Y qué importancia tiene esto?. Si ofrecemos esos datos a alguien para que, haciendo ingeniería inversa, reconstruya el puzzle y nos diga cuales eran las velocidades originales de cada una de las galaxias tabuladas, podria concluir erróneamente que dichas galaxias están dotadas mayoritariamente de velocidades de recesión si utiliza una fórmula Doppler distinta a la que hemos utilizado nosotros. Por ejemplo, si en lugar de las fórmulas (1) y (2), la cuales son completas porque son autosimilares, utiliza estas otras, la cuales son sólo una aproximación de primero orden de las anteriores:

	(3)
	(4)

llegará a la conclusión de que las galaxias (estadísticamente) se están alejando unas de otras. Pero, nosotros, que somos quienes hemos elaborado los datos iniciales, y se los hemos proporcionado a modo de acertijo, sabemos que las galaxias se mueven con velocidades aleatorias, tanto de acercamiento como de alejamiento. Sólo hay que pensar un poquito para darse cuenta de que todo esto de la expansión del universo es un camelo, producto de una alucinación por empecinarse en usar modelos matemáticos incorrectos.

Si, amigo lector de Tardígrados, el Big Bang nunca existió, ni la madre que lo parió tampoco. La expansión del universo es una patraña, un gran bulo que nos están metiendo. Cuando usas la Ley de Hubble para decretar a qué distancia debe estar una galaxia estás usando una herramienta ficticia que produce conclusiones engañosas. El método científico nos impide afirmar que sea siempre cierto que cuanto más alejada está una galaxia mayor es el corrimiento al rojo de su luz. ¿Qué pasa?. ¿Aún no te crees lo que te estoy contando?. ¿Aún piensas que, de verdad, el universo se expande y que, por lo tanto, una vez hubo un Big Bang?. Insistamos un poco más en todo esto. Desechemos la Ley de Hubble, de momento, como herramienta para catalogar distancias galácticas. Pensemos, como he hecho antes, que las velocidades de galaxias, quasares y cúmulos, se distribuyen uniformemente por el espacio como las partículas de un gas.

Pues bien, presentamos a nuestro investigador, una tabla con los corrimientos de una determinada longitud de onda, en concreto de la longitud de onda original λ₀ = 486 nm (nanómetros). Esta longitud de onda corresponde a la linea verde-azulada del espectro del átomo hidrógeno para la transición que va desde n=4 a n=2. Es decir, la energía de ese fotón emitido en esa transición atómica es de 2.55 eV (electrón-voltios). Como digo, a nuestro investigador de astrofísica, le vamos a presentar una tabla con 1000 valores de corrimientos al rojo de esa longitud de onda λ₀, que elaboraremos aplicando nuestra fórmula (2) de Doppler. Este es el gráfico de los puntos que representa las 1000 longitudes de onda:

El investigador, desde esta tabla, debe usar su fórmula Doppler para elaborar una tabla de velocidades. Y hemos supuesto ya que el investigador usará la fórmula Doppler incompleta (4). Con lo cual las velocidades que hallará serán las calculadas así:

(5)

La tabla de velocidades que hallaría sería esta:

Hemos asumido que la velocidad de la luz es c=1, y que las velocidades no superan dicha velocidad máxima. Observamos lo siguiente: aun siendo el número de velocidades de acercamiento hacia el observador aproximadamente igual al número de velocidades de recesión, vemos que las de acercamiento están más comprimidas en el intervalo [0, 0.6]. En cambio las velocidades de recesión están expandidas dentro de un intervalo más amplio, el [0, -1.6]. Si el investigador asume que la fórmula de Doppler empleada para deducir las velocidades es la correcta, entonces llegará a la conclusión de las galaxias que se alejan del observador lo hacen a mayor velocidad que las galaxias que se acercan.

Supongamos ahora que el investigador es muy avanzado y en lugar de la fórmula de Doppler anterior, usa la fórmula del Doppler relativista siguiente, que se supone es más precisa:

(6)

la cual al resolver para v, tenemos ;

(7)

y el gráfico de velocidades para esa distribución de 1000 longitudes de onda sería este:

Es decir, observando este último gráfico, el investigador vería incluso más distorsión que en el anterior, por lo que pensaría que las velocidades de recesión estarían en un intervalo incluso más amplio, el [0, -3.5], mientras que las velocidades de acercamiento estarían más apelotonadas en en intervalo [0, 0.5], casi apelotonadas alrededor del 0.

Por último, veamos qué ocurre cuando el investigador usa la misma fórmula Doppler que hemos usado nosotros para calcular la tabla de longitudes de onda que le hemos presentado. Es decir si usa la ecuación (2), las velocidades se deducen así:

(8)

y el gráfico para esta distribución de velocidades sería este:

y observamos cómo estas 1000 velocidades se distribuyen al azar uniformemente en un único intervalo [-1, 1], con lo cual el investigador sólo podrá concluir en este caso que las galaxias se acercan o se alejan aleatoriamente, sin poder extraer ninguna correlación significativa.

Saludos

Nuestro universo no es una simulación por ordenador pero tú sí

La física teórica actual nos lleva a divagar sobre cuestiones tan absurdas como por ejemplo “¿somos una simulación de ordenador?”. Lo peor de todo esto es que se lo toman en serio, se crean debates por televisión, conferencias, simposios, talleres, se escriben artículos, muchos artículos, y dicen que todo es un debate científico. La culpa de todo este sinsentido la tiene una teoría llamada Mecánica Cuántica. Esa teoría en la que se basa la metateoría llamada Modelo Estándar permite que nuestra imaginación explote y se expanda hacia terrenos inhóspitos y “absurdos”. En el modelo cosmológico estándar, también llamado, modelo Lambda-CDM, ó ΛCDM (en inglés es Lambda-Cold Dark Matter), sí, ese que usa la teoría del Big Bang, existe un pequeño cabo suelto desde el cual los divagadores pueden proponer que nuestro universo fue creado (diseñado) por alguien (¿Dios?), y que ese alguien no sólo se conformó con crearlo sino que se “divierte” observando su creación (nos observa). Incluso hay quien afirma, que no sólo observa su creación sino que interactua de vez en cuando con ella (¿milagros?).

Todo esto sería muy gracioso si no fuera porque muchos se lo toman muy en serio. A mi me gusta respetar todas las creencias religiosas, pero cuando la ciencia intenta suplantar la religión, me da un ataque de risa. Obviamente los rezos y plegarias de muchos creyentes van dirigidos a su Dios (el creador de la simulación por ordenador) para que interactue con ellos y solucione sus problemas. Desgraciadamente, en este universo no existe la magia, y los milagros brillan por su ausencia. Todo obedece a las leyes naturales (leyes de la física), las cuales son inviolables, inexcusables, inexorables. Cuando una piedra cae por causa de la gravedad universal desde lo alto de una montaña hacia el valle, no podrá ser detenida con rezos ni ruegos, sólo con algo dentro de la ley natural que perturbe su trayectoria.

Múltiples universos dentro de un fractal

Nuestro universo no es una simulación por ordenador, sino que es real, por una sencilla razón ontológica: todo tiene una causa real y natural, y no existen causas incausadas. Imagina un personaje virtual que evoluciona en un mundo virtual (tipo Matrix). ¿Cómo podría saber ese personaje que en realidad vive en un mundo virtual, simulado?.

Si algunos sustituyen la religión por la ciencia para afirmar que vivimos en una simulación de ordenador, yo me arrogo el derecho a usar la lógica y el discurso de Bertrand Russell para afirmar que:

La religión se basa, principalmente, a mi entender, en el miedo. Es en parte el miedo a lo desconocido, y en parte, como dije, el deseo de sentir que se tiene un hermano mayor que va a defenderlo a uno en todos sus problemas y disputas. El miedo es la base de todo: el miedo a lo misterioso, el miedo a la derrota, el miedo a la muerte. El miedo es el padre de la crueldad y, por lo tanto, no es de extrañar que la crueldad y la religión vayan de la mano. […] Tenemos que mantenernos en pie y mirar al mundo a la cara: sus cosas buenas, sus cosas malas, sus bellezas y sus fealdades; ver el mundo tal cual es y no tener miedo de él. Conquistarlo mediante la inteligencia y no solo sometiéndonos al terror que emana de él. Toda nuestra concepción de Dios es una concepción derivada del antiguo despotismo oriental. […] Un mundo bueno necesita conocimiento bondad y valor; no necesita el pesaroso anhelo del pasado, ni el aherrojamiento de la inteligencia libre mediante las palabras proferidas hace mucho por hombres ignorantes. Necesita un criterio sin temor y una inteligencia libre. Necesita esperanza en el futuro, no el mirar hacia un pasado muerto, que confiamos que sea superado por el futuro que nuestra inteligencia puede crear.

Siguiendo la lógica y el conocimiento que Russell desplegó en su obra Why I Am Not a Christian, podemos aportar al menos tres argumentos en contra de la afirmación “vivimos en una simulación”:

Contra el argumento cosmológico que afirma que existe una Causa Primera Universal, podemos alegar que en el terreno de la ciencia ese argumento tiene poco peso. Si todo ha de tener alguna causa, entonces Dios debe tener una causa. Por el contrario, si puede haber algo sin causa, entonces bien podría nuestro universo no haber necesitado causa alguna para existir (universo eterno e infinito), por lo tanto no sería necesario ningún Dios para explicar ni su existencia ni su evolución (en esto piensa actualmente Stephen Hawking)

Para el argumento de las Leyes Naturales, podemos afirmar que si existe alguna causa por la que Dios dictó esas leyes naturales, entonces él mismo debe estar sometido a esa causa o ley externa y por lo tanto, Dios mismo sería un intermediario. Pero, entonces Dios no nos sirve porque no es el último que dicta la ley. Este argumento tampoco se sostiene.

En cuanto al argumento teleológico, que es una especie de principio antrópico, el cual afirma que todo en el mundo está hecho para que podamos vivir en él, y si el mundo variase un poco, no podríamos vivir. Es decir, este argumento dice que el mundo y todos nosotros estaríamos dentro de un Plan Divino. Pero entonces ese Plan Divino sería una autentica mierda, viendo la miseria y el sufrimiento que hay en el mundo. ¿En realidad alguien se cree que este mundo ha sido creado para vivir en él?. Yo podría diseñar un mundo mas confortable y feliz, donde las enfermedades, el sufrimiento y los fanatismos, producto de la irracionalidad y la animalidad, no pudieran existir por ley natural. ¿Qué clase de Dios tan imperfecto creó este valle de lágrimas?, ¿para qué?. Este argumento teleológico o antrópico tampoco sirve, se cae por su propio peso y su ingenuidad.

En resumen. Nuestro universo no es ninguna simulación por ordenador, aunque se le pueda parecer. Es un valle de lágrimas, donde reina la injusticia, y el sufrimiento. En realidad, este universo es bastante inhóspito, y parece casi un milagro que pueda existir algo siquiera parecido a lo que llamamos vida. Desde un punto de vista científico, ó más exactamente desde la termodinánica, los organismos vivos son sistemas que tienden a disminuir su entropía, en supuesta perfecta contradicción a las “leyes naturales”. ¿Cómo?, ¿dónde surgió la vida?, ¿por qué? ¿Quién ordenó esto? son preguntas que sólo la ciencia y no religión debe responder. Evidentemente, el principo antrópico es una especie de ingenuidad institucionalizada, una auténtica bobería. ¿Se pregunta una ameba por qué existe ella o por qué el universo es como es?. Nuestro universo es como es y punto, y si fuera de otra forma también sería como es.

Saludos

BICEP2: triste ejemplo de mala investigación científica que casi roza el fraude

Hola amigos de Tardígrados. Hoy, en este breve artículo, os traigo algo que no deberia ocurrir muy a menudo en el mundo de la ciencia. Primero, se anuncia a bombo y platillo que se ha descubierto algo muy importante en el terreno científico, con el consiguiente revuelo mediático, y poco tiempo después a alguien se le ocurre revisar un poco el documento científico del tan “sonoro descubrimiento” y se percata de que tal vez dicho hallazgo podría quedar en nada debido a que la señal se desvanece en el ruido de fondo si se analizan corretamente los datos y los procedimientos.

No voy a entrar en detalles técnicos sobre el experimento BICEP2, tan sólo decir que “las afirmaciones audaces sobre fenómenos muy importantes para la ciencia necesitan estar respaldadas por evidencias también muy importantes” (bold claims require bold evidence)- Los resultados de ese experimento llamado BICEP2, venían nada menos que a decirnos que se había encontrado evidencia de ondas gravitacionales primordiales que confirmaban el modelo de inflación cósmica del Big Bang. Para hacer tan audaz afirmación estudiaron los B-modes de la Radiación Cósmica de Fondo. la cual es un tipo de polarización de la luz, el otro tipo son los E-modes.

Grosso modo, las conclusiones de este experimento BICEP2 son falsas porque se demuestra que no se usaron adecuadamente los mapas de fondo de ruido. No se tuvo en cuenta que el polvo galáctico genera B-modes que están a la par con la señal, y eso significa que BICEP2 afirma que lo observado es efecto de las ondas gravitacionales primordiales. Es decir, la falsedad de los resultados de BICEP2 consiste en que lo que se ha medido no es procedente de ondas gravitacionales primordiales, sino procedente del polvo galáctico. Una pena, señoras y señores. Lamentáblemente BICEP2 ha sido un suflé que se sacó demasiado rápido del horno, y acabó desinflándose. La teoría de inflación cósmica parece estar desinflándose como un suflé.

En el siguiente videoclip de youtube podeis ver cómo el profesor adjunto Chao-Lin Kuo de la Universidad de Standford se dirige a la casa del profesor Andrei Linde, el cual es uno de los creadores de la teoría de la inflación cósmica, para brindar con él por el feliz hallazgo de evidencias a favor de las ondas gravitacionales primordiales en BICEP2:

Por lo tanto, y para restaurar la simetría que fue rota por esa prematura celebración, aquí os dejo este otro videoclip que he creado hoy y al que le he puesto el título “Stanford Professor Andrei Linde retracts about the prematurely celebrated BICEP2 ‘physics breakthrough’ “:

Lo curioso del caso de BICEP2 es que aún siguen intentando engañar a la gente manteniendo como válidos esos resultados, pues nadie ha presentado una retractación oficial al respecto. Una pena, la verdad.

Saludos

Planck también ve “el eje del mal” en el Fondo Cósmico de Microondas

Estos días se habla mucho de los nuevos datos aportados por el satélite Planck. Aunque parece ser que muchos han quedado un poco defraudados, porque esperaban datos más contundentes.

Satélite Planck de la ESA

Andrei Linde, físico teórico ruso-norteamericano y profesor de física en la Universidad de Stanford, y uno de los proponentes de lo que se llama la inflación cósmica, dijo lo siguiente, mucho antes de que se conocieran los resultados del satélite Planck de la ESA:

“Si Planck descubre ondas gravitatorias, pondrá en primera plana todos estos modelos [de alta-energía]“

Pero, el satélite Planck no ha encontrado ondas gravitatorias. Linde también mostraba esperanza de que Planck demuestre o refute las problemáticas observaciones de WMAP (lease “eje del mal y otros horrores”). Es decir que el llamado “eje del mal”, si se demuestra que su origen es cósmico y no un sesgo sistemático, fastidiaría su teoría de la inflación cósmica. Pero, el satélite Planck no ha refutado “el eje del mal”, lo ve igual que lo veía la sonda WMAP de la NASA, o quizás lo ve aún con más nitidez.

Para cualquier “mainstreamófilo” (seguidor acérrimo de la doctrina oficial, fé ciega, acritico) el “eje del mal” es un horror porque pone en tela de juicio el dogma, la doctrina oficial, y eso no puede ser aceptado de ningún modo. Los acríticos de lo políticamente correcto luchan con todas sus fuerzas para desterrar para siempre ese horror y otros muchos. Pero ¿qué es el “eje del mal” y por qué jode tanto a los mainstreamófilos del lameculismo oficial?. En primer lugar el “eje del mal” se carga cualquier universo isótropo, es decir, el universo observable podría ser más largo en una dirección que en otra, y eso es un horror para el modelo estándar. También indicaría que existe un sistema de coordenadas preferente, lo cual se cargaría de un plumazo la relatividad especial de Einstein. También demostraría ese “eje del mal” que la velocidad de la luz en el vacío no es ninguna constante universal, con lo cual echaría mas tierra sobre la tumba de la relatividad Einsteniana.

La sonda WMAP antes que Planck fue la primera en ver patrones de puntos calientes y fríos en el fondo cósmico de microondas (CMB en inglés) que no están distribuidos al azar como se esperaba. En cambio, parecían estar alineados a lo largo de un eje, al que João Magueijo y su equipo en el Imperial College London (ICL) le pusieron el nombre de “eje del mal”.

Los cosmólogos estaban divididos sobre si el efecto era real o un defecto de los instrumentos de WMAP. Razonaban diciendo que si era real, entonces necesitarían revisar sus ideas de la forma del universo. El patrón observado podría significar que es más largo en una dirección que en la otra. Esto podría significar el cambio en los modelos de inflación —el período de expansión justo después del Big Bang— que postula un universo isótropo, que es igual en todas direcciones. Andrew Jaffe del ICL decía:

“Si vemos el eje del mal con Planck, entonces sabremos que no es un defecto del instrumento”

Pero, vayamos por partes (como dijo Jack “el destriprador”). El Fondo Cósmico de Microondas, como su propio nombre indica, son fotones cuya frecuencia está en el intervalo de lo que llamamos las microondas, es decir ondas electromagnéticas cuya frecuencias van desde los 300 MHz hasta los 300 GHz, lo que suponen longitudes de onda de entre 1 m a 1 mm. Dichos fótones proceden de los confines del universo observable. Es decir, proceden de nuestro horizonte cósmico. Se cree que más allá de donde proceden esos fotones no nos llega radiación de ningún tipo. Pues bien, cuando los cientificos distribuyen las frecuencias de dichos fotones en una gráfica, resulta que el plot obtenido es muy similar al del espectro de radiación de un cuerpo negro, que ofrece diferentes temperaturas, y cuya temperatura media sería de 2.725 K (Kelvin).

El espectro de la radiación de fondo de microondas medido por el instrumento FIRAS en el satélite COBE

Pero, obviamente la CMB no posee en sí misma ninguna temperatura, ya que no existe realmente una única fuente o hipotético cuerpo negro que emita esa radiación. La CMB está únicamente formada por simples y modestos fotones, que según qué teoria uses, su procedencia podrá ser el llamado Big Bang o cualquier otra cosa, quizás más prosaica, como por ejemplo la emisión de luz de átomos de Hidrógenos remotos, procedentes de nuestro horizonte cósmico que ha sufrido un corrimiento al rojo hasta llegar a los valores que se observan. Entonces, nuestra esfera celeste está llena de puntos desde los que nos llegan fotones de CMB, y cada punto en la esfera posee un color representativo de su diferencia de temperatura respecto a la media de 2.725 K

Este mapa de color que representa diferencias de temperatura de nuestra esfera celeste, y que representa a los fotones que nos llegan de la CMB, puede ser descompuesto en muchos otros mapas más simples. Esa descomposión se llama expansión en multipolos esféricos. Pero, ¿qué es exactamente una expansión en multipolos esféricos?. Si poseemos un mapa esférico que se puede describir mediante la función de dos variables , donde y son respectivamente el ángulo polar y el ángulo acimutal. Podemos expandir dicha función por medio de sumas de términos que implican a los llamados armónicos esféricos. Por ejemplo, esa función de dos variable la podemos expresar de la siguiente forma:

(1)

Donde: representan los armónicos esféricos, son los respectivos coeficientes de la expansión: El término representa la parte monopolar; Los términos representan la parte dipolar, etc.

Los armónicos esféricos son esencialmente funciones trigonométricas. Los físicos tienden a referirse a una descomposición en armónicos esféricos como “modos”. Así, el termino correspondiente a l=0 es un monopolo, para l=1 los términos son llamados dipolos, para l=2 cuadrupolos, etc. Una anisotropía dipolo de la temperatura de la CMB es una variación periódica la cual completa un ciclo alrededor del cielo Ese dipolo tiene un polo “caliente” y un polo “frio”. Una anisiotropía cuadrupolar es una variación periódica de la temperatura de la CMB la cual completa dos ciclos alrededor del cielo. En general una anisotropía de modo l del cielo completa l ciclos alrededor del cielo. Despues de sustraer los efectos de la rotación diurna de la Tierra, su órbita alredor del Sol, el movimiento de transalación del Sol en la Vía Láctea, y el movimiento de la Vía Láctea en el Grupo Local, observamos desde la Tierra una anisotropía dipolar de la CMB en la esfera celeste. Esa anisotropía dipolar en nuestra esfera celeste se debe al movimiento propio del Grupo Local de galaxias hacia el supercúmulo de Virgo, a una velocidad de de aproximadamente 600 km/s. Esa anisotropía dipolar de la temperatura se sustrae de la CMB, con lo cual queda un patrón de temperatura que debería ser isótropo estadísticamente.

Desafortunaddamente, parece que los modos de cuadrupolo y octupolo de la CMB (modos con l=2 y l=3) son cualquier cosa menos isótropos. Sus respectivos ciclos de puntos de calor y frio sólo están presentes en un particular plano del cielo, y los ejes de esos dos planos están estrechamente alineados entre sí. Es muy intrigante también que estos ejes apunten hacia la dirección general del supercúmulo de Virgo. Si estos alineamientos ocurren por azar, entonces sus probabilidades serian de 0.015 y de 0.05 respectivamente.

Peor aún. Michael Longo de la universidad de Michigan analizó 1660 galaxias espiral en los catálogos del Sloan Digital Sky Survey, y encontró que sus ejes de rotación están casi alineados con “el eje del mal” (su paper en arxiv fue retractado más tarde, parece ser). Longo estima que la probabilidad de que esto ocurra por azar es menos del 0.4 por ciento.

Las fluctuaciones en la CMB de las escalas angulares mas grandes se cree que son restos de las fluctuaciones de densidad primordiales. El “eje del mal” es por lo tanto un serio problema para la teoría de la inflación.

Sin embargo, hay que recalcar que la cosmología basada en la relatividad general es perfectamente capaz de asumir un universo no-isótropo. Aunque los modelos de la FRW son perfectamente de simetría esférica alrededor de cada punto espacial, existe otra clase de modelos espacialmente homogeneos los cuales sólo son rotacionalmente simétricos sobre cada punto. Entre estos últimos está la clase Kantowski-Sachs. Mientras que el grupo de isotropía espacial de un modelo FRW es SO(3), el grupo de isotropía espacial de un modelo de simetría rotacional es SO(2). Estos modelos de simetría rotacional son también homogeneos , por lo tanto cada punto del espacio es rotacionalmente simétrico alrededor de un eje.

Hasta ahora, todo intento de explicar “el eje del mal” como consecuencia de la contaminación de datos de la CMB por procesos cercanos de primer plano (locales) ha resultado infructuoso. De todas formas, el hecho de que “el eje del mal” apunte hacia el supercúmulo de Virgo parecería ser también una coincidencia bastante remarcable si ocurriera por azar. Quizás procesos locales, relacionados con el movimiento del Grupo Local hacia el supercúmulo de Virgo han alterado la anisotropía dipolar. La consecuencia quizás sea que no hemos sustraido correctamente la anisotropía dipolar de la CMB, con lo cual quedan restos viciados en los modos de cuadrupolo y octupolo.

Planck mapea la noche de los tiempos

En mi opinión “el eje del mal” se debe básicamente a que la velocidad de la luz en el vacio es variable, pues esa variación depende de la velocidad de la fuente respecto del observador. Esta anomalia, la cual no sé por qué estúpida razón fue bautizada como “eje del mal”, está muy relacionada con un antiguo e histórico experimento, el cual ha sido denigrado y menospreciado. Ese experimento fue el de Dayton Miller. El vió antes que nadie el llamado “eje del mal” y cómo la velocidad “absoluta” de la Tierra apunta hacia el supercúmulo de Virgo. Maurice Allais pudo efectuar mucho después un minucioso análisis estadístico sobre los datos del experimento de Dayton Miller y pudo descubrir cómo existen alineaciones no fortuitas con la ecliptica.

Seis básicos para una alerta de tardígrados panspérmicos

1. ¿Cómo, cuándo y de dónde llegaron los tardígrados al cometa Halley?.
   
   

2. Si el bosón de Higgs existe, entonces el tamaño del universo coincide con el tamaño  de un huevo de avutarda.
   
   

3. Si la teoria de la relatividad de Einstein, en especial la teoria de la relatividad especial, es cierta, entonces uno de mis dos gemelos es más viejo que el otro.
   
   

4. La matería oscura es tan oscura porque se han emperrado en que la teoría general de la relatividad de  Einstein tiene que ser cierta por huevos, cuando lo más fácil sería pensar que seguimos sin tener ni pajolera idea de lo que es la gravedad.
   
   

5. Se han descubierto galaxias a menos de 400 millones de años del Big Bang. No sabía yo que a las galaxias le salieran las tetas tan pronto.
   
   

6. Hace más de cincuenta años que se sabe que el universo se expande aceleradamente. Desde entonces, el universo ha conseguido expandirse exactamente al mismo tamaño que tenia entonces.