Hola amigos de tardígrados. Hoy vamos a aprender a hacernos ricos en poco tiempo 🙂 En este pequeño tutorial aprenderemos cómo minar
bitcoins desde cero, burlando así a las grandes granjas chinas de minería de criptomonedas.

Quizás yo no sea muy bueno en muchas cosas, pero con los años aprendí a conocerme a mi mismo bien, y descubrí que tengo ciertos talentos ocultos. Una de esas destrezas, que tenía oculta, es que soy capaz de adivinar cualquier contraseña en menos de un minuto sólo con el poder de mi mente 😛 ¿No te lo crees?. Mándame una dirección de correo electrónico tuya, y verás en tu sección de correos enviados, cómo, en poco tiempo (dependiendo del número de solicitudes de incrédulos), “me habrás enviado” un correo electrónico a
albertzotkin@yahoo.com, en el que me dirás lo siguiente:
“Esto prueba que sé tu contraseña y usé tu dirección de correo para enviarme esto”. Sí, amigo de Tardígrados, yo soy un superhéroe los días pares, y los impares un villano. A parte de esa destreza de adivinar mentalmente contraseñas, la cual resulta bastante sorprendente, teniendo en cuanto que soy un humano, también tengo otras cualidades ocultas, más sorprendentes aún que esa, si cabe, pero no te las voy a decir de momento, para que sigan siendo ocultas.
Hoy en día existen muchas
criptomonedas, la mayoria están basadas en la tecnología del
blockchain. Hasta la tostadora
IoT que tengo en mi casa sería capaz de crear una criptomoneda. Sólo hay que ver que hasta Nicolás Maduro fue capaz de crear la
criptomoneda Petro, con eso está dicho todo.
En este pequeño artículo que estoy escribiendo, me voy a centrar solo en el
bitcoin. Hoy en día es posible comprar y vender bitcoins fácilmente, con lo que tú solito puedes llegar a enriquecerte, o a arruinarte a placer, especulando con esa moneda electrónica tan volátil. Las ventajas que tiene el bitcoin y otras monedas electrónicas, son que es un sistema descentralizado, y puede escapar fácilmente del fisco, pero a cambio, estás a expensas de fraudes, robos, y demás actividades encaminadas por terceros a dejarte sin dinero en tu billetera a cambio de nada más que disgustos. Pero, como vamos a partir de cero, es decir, de cero euros, nuestro disgusto de que nos roben cero euros sería menos del que sufriríamos si partiéramos de nuestros ahorros de toda la vida, o del dinero de la cesta de la compra.
Pero vayamos ya sin más tardar, al ajo. Para poder hacernos ricos con el bitcoin, lo primero que tenemos que hacer es conseguir una billetera (no digo monedero, porque hay ciertas personas con ciertos apellidos que me caen mal). Para ganar nuestro primer bitcoin, que a día de hoy esta a 8212.96 € en el mercado cambiario, tendremos nuestra billetera preparada para recibir moneditas calenticas recién minadas. La mejor billetera que puedes conseguir es la
electrum. Una vez que hayas creado tu billetera de bitcoin electrum, guardarás tus claves offline, fuera del sistema, para que nadie que no seas tú, pueda hacerse con ellas y desplumarte. La electrum crea una clave muy peculiar, desde la que puedes acceder a tu billetera desde cualquier parte que posea conexión a internet, o con una única contraseña si la usas localmente desde tu dispositivo habitual. Dicha clave consiste en una secuencia ordenada de 12 palabras. Esa secuencia ordenada la puede memorizar, o la puedes guardar donde te plazca, pero siempre fuera del alcance de curiosos. Yo, por ejemplo, la clave de mi billetera electrum la tengo memorizada, pero también me hice un pictograma con esas 12 palabras de mi clave, porque a veces mi memoria me falla. El pictograma mnemotécnico de mi clave electrum, donde guardo algunos bitcoins, es este:

Si sientes el deseo que robarme mis criptomonedas, sólo tienes que adivinar a qué palabra corresponde cada uno de esos iconos, y voila!. Pero, si lo que deseas es enviarme algunos Satoshis, puedes hacerlo a mi clave publica:

un Satoshi es la cien millonésima parte de un bitcoin = 0.00000001 BTC. O sea que si un bitcoin se cambia actualmente por 8212.96 €, entonces 1 euro serían 12175.87 Satoshis. Lo de comprar y vender bitcoins, o con bitcoins, no tiene mayor misterio. Como habrás comprobado ya, incluso a la hora de recibir o enviar bitcoins con electrum, lo podemos hacer mediante los famosos códigos QR desde nuestros teléfonos móviles. Entonces, te estarás preguntando, cómo y cuándo vamos a empezar ya de una vez a ganar nuestros miles de Satoshis. La respuesta está en la minería de bitcoins.
La minería de bitcoins es una actividad mediante la cual van agrupando las nuevas transacciones en bloques, y estos bloques se unen a la gran cadena de bloques o blockchain. Los mineros usan potentes maquinaria de hardware a gran escala, para conseguir algún provecho, de lo contrario, esa actividad no sería rentable. Los mineros se comunican unos con otros mediante una red de nodos P2P, peer-to-peer. Usualmente lo hacen con el protocolo TCP estándar, el de los servidores web, pero no por el puerto 80 habitual, sino por los puertos 8333 o el 8332. Estos mineros de criptomonedas usan factorías llenas de cientos de procesadores fabricados y dedicados expresamente a realizar una única y sencilla operación matemática, pero han de hacerlo a gran velocidad para tener algo de probabilidad de encontrar la solución en un tiempo razonable para la rentabilidad económica. El problema con esos dispositivos es que, cada uno de ellos, es un monstruito muy ruidoso, bastante tragón de energía eléctrica, y se calienta bastante. Si juntamos en una nave industrial cientos de esos monstruitos computando a la vez sin parar las 24 horas del día, lo que obtenemos es una actividad super contaminante de ruido y calor, con energía desaprovechada por un tubo. La factura de la luz de un sólo día puede llegar a alcanzar miles de euros. La recompensa por resolver un bloque de transacciones de bitcoins es de algunas monedas, suficiente para conseguir rentabilidad.
¿En qué consiste esa sencilla operación matemática que tienen que realizar a toda velocidad esos procesadores para conseguir hacer negocio?. La solución de esa rutina operacional se llama
Prueba de Trabajo. Los mineros, recolectan un conjunto de últimas transacciones del día, que están por ser confirmadas (validadas), y con ese conjunto de transacciones construyen un proyecto de bloque para ser añadido e integrado en la cadena blockchain. Junto a esas transacciones redactan la suya propia (transacción
coinbase) para ganar la recompensa en el momento de dar con la solución, y todo irá incluido en el mismo proyecto de bloque. Pongamos un ejemplo concreto. Hace unos momentos, a las 17:55 de la tarde (hora de Benidorm 🙂 ), unos mineros chinos del pool
AntPool han conseguido cuadrar (resolver) un nuevo bloque. Exactamente uno con el
hash = 000000000000000000044b6c80648ead63c9ab7cad89f7841d6c1a420d34ba43. ¿Que qué es un hash?. Un hash es simplemente algo muy parecido a la huella de una cadena de caracteres. Existe una función hash256 que se aplica, para nuestro caso concreto, dos veces (iteración) sobre una cadena de 80 caracteres, correspondiente a la cabecera del bloque proyecto que proponen los mineros. Este bloque hallado es el número 614930 dentro del blockchain. Estos mineros chinos, en su granja con sus miles de “gallinas cibernéticas”, cacareando calientes sin parar, han puesto un huevo, por el que se están llevando al bolsillo 12.5 bitcoins, más una comisión de 0.2, es decir, un total de 12.7 bitcoins = 104304.6 euros (y eso lo hacen cada día, unas cuantas veces). La cabecera de 80 bytes, codificada en binario, de ese bloque es la siguiente:
|
0000000h : 00 00 00 20 9d 88 e1 40 67 f7 f0 10 db 58 5a 2f ; ... ...@g....XZ/
0000010h : d7 28 bb c2 d8 1e e3 09 64 b7 0b 00 00 00 00 00 ; .(......d.......
0000020h : 00 00 00 00 82 e4 1c d2 3e c9 9f 27 d0 66 27 99 ; ........>..'.f'.
0000030h : c0 cc 88 11 35 1e 33 ed d0 33 6c bd 3c b5 11 79 ; ....5.3..3l.<..y
0000040h : 68 a5 e4 5e 9b 67 30 5e ff 32 12 17 74 c7 f9 01 ; h..^.g0^.2..t...
|
Si desglosamos la estructura de esa cabecera de 80 bytes, veremos qué parámetros la forman:
$version = 536870912
$previous_block = 0000000000000000000bb76409e31ed8c2bb28d72f5a58db10f0f76740e1889d
$merkle_root = 5ee4a5687911b53cbd6c33d0ed331e351188ccc0992766d0279fc93ed21ce482
$time = 1580230555
$nbits = 387068671
$nonce = 33146740
|
Si ahora aplicamos la función hash256 dos veces sobre la cadena en binario de esos 80 bytes de la cabecera, obtenemos lo siguiente:
|
hash256(hash256(cabecera))=
000000000000000000044b6c80648ead63c9ab7cad89f7841d6c1a420d34ba43
|
que coincide exactamente con el hash del bloque encontrado por los mineros del Antpool. Esto significa que hemos comprobado por nosotros mismos que ese block es válido. Ya de entrada, notamos algo raro en el hash de ese bloque. Los hash256 son todos cadenas alfanuméricas (aparentemente aleatorias, porque no hay manera de saber a qué cadena de caracteres corresponde un hash determinado) de exactamente 64 caracteres, o lo que es lo mismo, de 32 bytes (independientemente del número de caracteres de la cadena sobre la que se aplica). En realidad, vemos que todo hash es un número expresado en base hexadecimal. Lo raro que notamos, es pues que existan tantos ceros seguidos a la izquierda de ese hash, de hecho es muy raro que un hash256 empiece siquiera por un único cero. En realidad, esa rareza de muchos ceros al inicio del hash es precisamente lo que se busca con tanta codicia por los mineros. Los dos parámetros clave para los mineros son el nbits y el nonce. Este ultimo es un valor que el minero está autorizado a cambiar, para ir probando hasta hallar un hash que tenga muchos ceros al inicio y que cumpla una condición. La condición la dicta el parámetro nbits. Mediante una sencilla operación el nbits se transforma en un número en base hexadecimal llamado target. Para el caso concreto del ejemplo de bloque que estamos analizando, como nbits = 387068671, el target, con esa sencilla operación, resultará ser
|
target=1232ff0000000000000000000000000000000000000000
|
Como tanto el hash del bloque como el target son números enteros (expresados en base hexadecimal, pero números), la condición, que exige Prueba de Trabajo es una simple pregunta: ¿Es el hash del bloque menor que el target?. Para contestar afirmativamente a esa pregunta los mineros empiezan a calcular el doble hash256 de la cabecera, desde nonce = 0. Y la palabra Bingo! suena bien alto en la sala cuando se halla un hash que es menor que el target.
En nuestro caso, para un nonce = 0, obtendríamos un doble hash256 de:
|
hash256(hash256(cabecera))=
a625bbfaf77163b53d1e30c30e8d01a7b0e00fb396b08f475d1c3eda7ecaf133
|
Es fácil ver que ese hash es mayor que el
target. Por lo tanto, un bloque con ese nonce = 0 no sería un bloque válido. Es imposible saber qué valor de nonce cumpliría la condición. En nuestro ejemplo el nonce = 33146740 hace que se cumpla la condición, y por la tanto el bloque queda validado.Todo es puro azar, una lotería, vamos. Cuanto más juegues a la lotería más probabilidad tienes de que te toque. En eso consiste la minería de criptomonedas, con trastos
ASIC, tragando hashes a velocidades endiabladas. Ludopatía pura y dura.
La velocidad de los procesadores mineros debe ser muy alta si quieren conseguir rentabilidad. Actualmente se usan en las granjas de minería de bitcoins esos chips tipo
ASIC. En cada granja puede haber instalados cientos de esos ruidosos aparatos. Compremos uno de esos aparatos y pongámonos a minar bitcoins por nuestra cuenta. Podemos adquirir uno baratito por 100 euros, el
AntMiner S7

Este aparatito tiene una velocidad de cálculo de 4.73 TH/s, es decir, 4.73 x 1012 hashes por segundo, pero chupa electricidad por un tubo, ya que consume con una potencia eléctrica de 1210 vatios. Teniendo en cuenta que en España el precio del kilovatio-hora es aproximadamente de unos 0.13 euros, ese aparatito, por sí solo, durante 1 día consume 29040 kilovatios-hora, es decir, un coste por día de 3.7 euros.
¿Cuál es la probabilidad de que a la primera obtengamos un doble hash256 que cumpla esa condición de ser menor que el parámetro target?. Es como tirar un dado y ver si obtenemos un 6 a la primera tirada, pero en el caso de los hashes existirían muchos más lados que los seis de un dado normal. ¿Cuántos exactamente?. El máximo número entero de 64 cifras en representación de base hexadecimal es este:
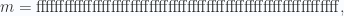
y si lo expresamos en base decimal obtendremos el número de 81 cifras

Esto significa que el número de caras de ese supuesto dado gigantesto sería de n+1. El target que se usó en el hallazgo de la solución para ese bloque era, como he dicho antes,
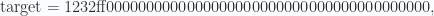
que expresado en base decimal es

Esto significa que la probabilidad de que un hash256 sea menor o igual a ese target es precisamente
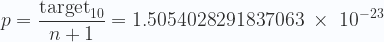
Nuestro aparatito para minar (el AntMiner S7) tiene una velocidad de v = 4.73 TH/s, por lo tanto, en un día, la probabilidad de resolver ese bloque sería de
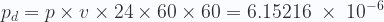
Si no me he equivocado en los cálculos, resulta ser una probabilidad demasiado baja, se necesitaría un promedio de 445 años para hallar la solución. ¿Entonces, cómo podemos ganar dinero nosotros si no nos unimos a uno de esos pool de minería?. Parece obvio que, por nuestra cuenta, las probabilidades de obtener ganancias están muy próximas a cero. De hecho los mineros en pools incluso, a veces, agotan todos los nonces, y necesitan incluir extra nonces en los proyectos de bloque para seguir probando suerte.
Y hasta aquí puedo escribir … 😛 … de momento.







