TARDÍGRADOS

Ciencia en español -ʟᴀ ʀᴀᴢóɴ ᴇsᴛá ᴀʜí ғᴜᴇʀᴀ-

Posts Tagged ‘división’

El mundo de los muertos y la cinemática de los walking dead (Mecánica estadística)

Posted by Albert Zotkin on October 25, 2014

El “mundo de los muertos” es el infra-mundo de orden -1. En ese universo, las cosas son, se mueven y evolucionan de una forma muy peculiar. El “mundo de los muertos” es el reino de los objetos y fenómenos cuánticos por antonomasia. Por otro lado, la definición de función de partición en mecánica estadística es muy importante.

En un sistema de partículas en equilibrio que sólo intercambia energía térmica con su entorno, tenemos que la función de partición para dicho sistema es:

\displaystyle \mathcal{Z} = \sum_{s} e^{\beta \epsilon_s} (1)
donde la suma se ha realizado sobre todos los microestados s, εs representa la energía del microestado s y ß se define como menos el inverso del producto de la temperatura por la constante de Boltzmann:

\displaystyle \beta = -\frac{1}{k_BT}
Así desde estas definiciones podemos por ejemplo expresar la ecuación de estado de los gases ideales así:

\displaystyle \langle PV\rangle=-\frac{\ln(\mathcal{Z})}{\beta} = -\frac{\epsilon_1\oplus\epsilon_2\oplus\epsilon_3\oplus\dots}{\beta} (2)
donde εi representa la energía del microestado i. Es decir, la energia PV de los gases nobles es simplemente la infra-suma ⊕ de orden -1 de las distintas energias de los micro-estados. En general, toda ecuacion en la que aparezca el logaritmo de la función de partición, ln(Z), implica una infra-suma de energias de micro-estados. Pero alguien diría, muy bien y ¿dónde está el mérito de todo esto?. Pues el mérito de todo esto está en darse cuenta de que la infra-suma de orden -1 de energias de micro estados genera la emergencia de la energia del sistema macroscópico. Clásicamente la energía es una magnitud escalar que se suma o se resta canónicamente, con la aritmética de orden 0, pero lo curioso de todo esto es que las energias de los micro-estados se suman y se restan mediante la aritmética de orden -1. O sea, el macrocosmos (orden 0) emerge como consecuencia de infra-interacciones de orden -1.

infra Saludos

Posted in Física de partículas, Matemáticas, Mecánica Cuántica | Tagged: , , , , , , , , , , , , , , , , , , , , , , , | Leave a Comment »

Energía total y momento de una partícula expresados con infra-sumas

Posted by Albert Zotkin on October 20, 2014

Todos sabemos, o deberíamos de saber ya a estas alturas del curso, que la energía total y el momento de una partícula de masa m, que se está moviendo a cierta velocidad v, se expresan así:

\displaystyle E= mc^2 \cosh \left(\beta \right) \\ \\ p = mc\sinh \left(\beta\right) \\ \\ (1)

Donde β = v/c. Por otro lado, ya sabemos, o deberiamos de saber, que la infra-suma e infra-resta de orden -1 se definen así:

\displaystyle x \oplus y =\log(\exp(x) +\exp(y))\\ \\ x \ominus y =\log(\exp(x) -\exp(y)) (2)
Por lo tanto, la energía total y momento de una partícula se expresa con infra-sumas así:

\displaystyle E = \tfrac{1}{2} mc^2 \exp \left(\beta \oplus (-\beta)\right) \\ \\ p = \tfrac{1}{2} mc \exp \left(\beta \ominus (-\beta)\right) (3)
Y si exploramos un poco sobre la mecánica de las partículas en este infra-mundo, veremos cosas muy sorprendentes. Por ejemplo, en este infra-mundo de orden -1, la opuesta v’ a una velocidad v no sería –v, sino v’ = v + icπ, es decir una velocidad compleja cuya parte imaginaria sería el producto de dos constantes, cπ. Evidentemente, si infra-sumamos una velocidad v con su opuesta v’ = v + icπ, obtenemos el elemento neutro de la infra-suma de orden -1, que es -∞

\displaystyle v \oplus v' =\log(\exp(v) +\exp(v + ic\pi))\\ \\ v \oplus v' =\log(\exp(v)(1 +\exp( ic\pi))\\ \\ v \oplus v' =\log(\exp(v)(1 - 1)\\ \\ v \oplus v' =\log(0)=-\infty\\ \\ (4)
Eso nos hace pensar, en el ámbito de la relatividad, que quizás cuando una partícula (o cualquier cuerpo con masa) acelera desde cualquier velocidad infra-lumínica v < c, nunca llegaría a alcanzar dicha c, porque lo que ocurriría es que la velocidad se conjuga pasando de ser real a ser compleja cuyo valor sería v + icπ

Saludos

Posted in Física de partículas, Matemáticas, Mecánica Cuántica, Relatividad | Tagged: , , , , , , , , , , , , , , , , , , | Leave a Comment »

Elementos neutros y opuestos en las aritméticas de distintos órdenes

Posted by Albert Zotkin on October 5, 2014

Hoy voy a escribir un corto apunte sobre cómo calcular el elemento neutro de la suma de una aritmética de orden n si sabes cuál es dicho elemento en la aritmética de orden (n+1). Llamemos en a dicho elemento neutro de la suma ⊕n de orden n. Entonces tendremos que

\displaystyle e_n = \log(e_{n+1}) (1)
Por ejemplo: la multiplicación es la suma de orden 1, y su elemento neutro es el número natural 1. Entonces el elemento neutro de la suma ordinaria (suma de orden 0) es:

\displaystyle e_0 = \log(e_1)= \log(1)=0 (2)
como todos sabemos. El elemento neutro de la infra-suma de orden -1 es:

\displaystyle e_{-1} = \log(e_0)= \log(0)=-\infty (3)
Si ya sabemos calcular el elemento neutro, es fácil calcular el opuesto x’ de cualquier número x:

\displaystyle x \oplus_{n} x' =\log(e_{n+1}) (4)
y como sabemos que la suma de dos números x, y es:

\displaystyle x \oplus_{n} y =\log(\exp(x) \oplus_{n+1} \exp(y) ) \\ \\ (5)

tendremoa que:

\displaystyle \log(\exp(x) \oplus_{n+1} \exp(x'))= \log(e_{n+1}) \\ \\ \exp(x) \oplus_{n+1} \exp(x')= e_{n+1} \\ \\ (6)
Por ejemplo, usemos la suma ordinaria (orden 0) para calcular el opuesto x’ de orden -1 de un número x:

\displaystyle \exp(x) + \exp(x') = 0 \\ \\ \exp(x') = 0 - \exp(x) \\ \\ x' = \log(0 - \exp(x)) = x+ i \pi (7)
es evidente que x’ = x + i π es el opuesto de x en la suma de orden -1, ya que

\displaystyle x \oplus_{-1} (x+ i\pi) = \log(\exp(x) +\exp(x+ i\pi))= \\ \\ \log(\exp(x)(1+ \exp(i\pi)) = \log(\exp(x)(1-1)) = \log(0)=-\infty (8)
Sigamos con un poco más. El elemento neutro de la suma de orden 2 es e (la base de los logaritmos naturales), ya que

\displaystyle e_1 = \log(e_2) \\ \\ 1=\log(e_2) \\ \\ e_2 = e^1 =e (9)
El opuesto x’ de un número x para dicha suma de orden 2 sería pues un número tal que:

\displaystyle x\oplus_2 x' = e (10)

es decir,

\displaystyle x\oplus_2 x' =\exp(\log(x)\oplus_1 \log(x')) = e \\ \\ \exp(\log(x) \log(x')) = e \\ \\ \log(x) \log(x') = \log(e) \\ \\ x'^{\log(x)} =e \\ \\ x' = e^{1/\log(x)} (11)

Saludos

Posted in Matemáticas | Tagged: , , , , , , , , , , , , , , , | Leave a Comment »

La identidad de Euler como suma de opuestos del inframundo

Posted by Albert Zotkin on September 8, 2014

Hola incondicionales de Tardígrados. Hoy voy a escribir un pequeño apunte sobre la identidad de Euler, y de cómo puede ser expresada como una suma de opuestos de orden -1. La suma y la resta de orden -1 quedó definida en mis últimos dos posts de esta forma:

\displaystyle x \oplus y =\log(\exp(x) + \exp(y) ) \\ \\ x \ominus y =\log(\exp(x) - \exp(y) ) (1)

La identidad de Euler sabemos que es:

\displaystyle e^{\mathrm{i}\pi} =-1 \,\! (2)
Por lo tanto, pasando el -1 a la parte izquierda de la ecuación queda

\displaystyle e^{\mathrm{i}\pi}+1 = 0 (3)
es decir, podemos escribir la identidad de Euler así:

\displaystyle e^{\mathrm{i}\pi}+e^{0}= e^{-\infty} (4)
El opuesto en la suma de orden -1 de un número real x es un número complejo x’ cuya parte real es x, y cuya parte imaginaria es π. Con lo cual la suma de orden -1 de x con su opuesto x’ siempre dará el elemento neutro de esa suma de orden -1, es decir:

\displaystyle x \oplus x' =-\infty (5)

ya que -∞ es dicho elemento neutro de la suma de orden -1. Esto significa, que podemos escribir la identidad de Euler así

\displaystyle 0 \oplus i\pi = -\infty (6)
porque en general la suma de un número y su opuesto siempre es el elemento neutro de dicha suma. Y en el caso de la suma de orden -1 siempre tenemos que:

\displaystyle x\oplus (x + i\pi) = -\infty (7)

Saludos

Posted in Matemáticas | Tagged: , , , , , , , , , , , , , | Leave a Comment »

Aritmética del inframundo y del ultramundo

Posted by Albert Zotkin on August 24, 2014

Definamos la suma y la resta como operadores aritméticos de orden cero, que escritos con subíndices serian:

\displaystyle + = \oplus_0 \\ \\ -= \ominus_0 \\ \\ (1)

Así, la multiplicación y la división serian operadores de orden 1, y los escribiriamos así:

\displaystyle \times = \oplus_1 \\ \\ /= \ominus_1 \\ \\ (2)
En cuanto a la infrasuma y la infrarresta, que definí en mis dos anteriores posts, aqui y aqui, sus operadores escritos con subíndices serían de orden -1. Por lo tanto, toda operación aritmética de orden k puede ser expresada mediante operaciones aritméticas de orden inmediato superior k+1, así:

\displaystyle x \oplus_k y =\log(\exp(x) \oplus_{k+1} \exp(y) ) \\ \\ x \ominus_k y =\log(\exp(x) \ominus_{k+1} \exp(y) ) (3)
Supongamos que tenemos curiosidad por saber cómo son los operadores suma y resta inframundados de orden -2. Escribimos:

\displaystyle x \oplus_{-2} y =\log(\exp(x) \oplus_{-1} \exp(y) ) \\ \\ x \ominus_{-2} y =\log(\exp(x) \ominus_{-1} \exp(y) ) (4)
y si queremos expresarlos en función de la suma y la resta de orden 0, como sabemos que

\displaystyle x \oplus_{-1} y =\log(\exp(x) + \exp(y) ) \\ \\ x \ominus_{-1} y =\log(\exp(x) - \exp(y) ) (5)

tendremoa que

\displaystyle x \oplus_{-2} y =\log(\log(\exp(\exp(x))) + \exp(\exp(x)))) \\ \\ x \ominus_{-2} y =\log(\log(\exp(\exp(x))) - \exp(\exp(x)))) (6)
Cabe también preguntarse cómo se expresa una operación aritmética de orden k en función de su operadores de orden inmediato inferior, k-1. La respuesta es sencilla:

\displaystyle a \oplus_k b =\log(\exp(a) \oplus_{k+1} \exp(b) ) \\ \\ \exp(a \oplus_k b) =\exp(a) \oplus_{k+1} \exp(b) \\ \\ x= \exp(a) \\ \\ y=\exp(b) \\ \\ a= \log(x) \\ \\ b=\log(y) \\ \\ x \oplus_{k+1} y = \exp(\log(x) \oplus_k \log(y)) (7)
Ahora podríamos hacernos la misma pregunta que antes, pero hacia arriba. ¿Cómo expresamos una operación aritmética ultramundana de orden 2 con los operadores de orden inferior?:

\displaystyle x \oplus_{2} y = \exp(\log(x) \oplus_1 \log(y)) \\ \\ x \oplus_{1} y = \exp(\log(x) + \log(y)) \\ \\ \\ \\ x \oplus_{2} y = \exp(\log(x) \log(y)) \\ \\ x \oplus_{2} y = x^{\log(y)} (8)

o también

\displaystyle x \oplus_{2} y = y^{\log(x)} (9)

Lo cual produce el notable resultado:

\displaystyle x^{\log(y)} = y^{\log(x)} (10)

que siempre es cierto para cualesquiera números reales x e y.

Una resta de orden 2 sería asi:

\displaystyle x \ominus_{2} y = \exp(\log(x) \ominus_1 \log(y)) \\ \\ x \ominus_{1} y = \exp(\log(x) - \log(y)) \\ \\ \\ \\ x \ominus_{1} y = \exp \left (\log \frac{x}{y}\right ) \\ \\ x \ominus_{1} y = \frac{x}{y} \\ \\ x \ominus_{2} y = \exp \left (\frac{\log(x)}{\log(y)}\right ) \\ \\ \\ \\ x \ominus_{2} y = \left (x \right )^{\frac{1}{\log(y)}} (11)

Saludos

Posted in Matemáticas | Tagged: , , , , , , , , , , , | Leave a Comment »

La función Infra-Zeta de Riemann

Posted by Albert Zotkin on August 22, 2014

Hola amigos de Tardígrados. Hoy voy a continuar con el tema de las infrasumas e infrarrestas que definí en mi post anterior. Dichas definiones eran así:

\displaystyle x \oplus y = x+\log \left (1 + \exp (y-x) \right ) \\ \\ x \ominus y = x+\log \left (1 - \exp (y-x) \right ) (1)

en realidad hay una forma más sucinta de definir ambas operaciones, y es esta:

\displaystyle x \oplus y = \log \left (\exp (x)+\exp (y) \right ) \\ \\ x \ominus y = \log \left (\exp (x)-\exp (y) \right ) (2)

Vemos pues que el elemento neutro de la infrasuma es u = -8 (menos infinito):

\displaystyle x \oplus u = u \oplus x = x \\ \\ x=\log \left (\exp (x)+\exp (u) \right ) \\ \\ \exp(x) = \exp (x) + \exp (u) \\ \\ 0 = \exp (u) \\ \\ u = \log(0)= -\infty (3)

Igualmente, desde la definición de infrarresta podemos ver que cada número real x posee un opuesto x’ tal que:

\displaystyle x \oplus x' = \log \left (\exp (x)+\exp (u) \right )=-\infty (4)

es decir:

\displaystyle x \oplus x' = -\infty \\ \\ (x \oplus x') \ominus x = (\exp (x) + \exp (x'))= -\infty \ominus x = x \\ \\ x \oplus x' = \exp (x) + \exp (x') = -\infty \\ \\ (4)
que es un numero complejo con parte imaginaria π. En realidad para cada número real x existen infinitos números opuestos con parte real igual a x, y parte imaginaria nπi, donde n es un entero impar.

Podemos seguir y definir la operación multiplicación ⊗ así:

\displaystyle x \otimes n = \underset{n}{\underline{x \oplus x \oplus \dots \oplus x}} = \log(n \exp(x)) (5)
donde n es de momento un número entero, pero vemos que no es una operación conmutativa, ya que por regla general no es cierto que x⊗n = n⊗x. Intentemos, de todas formas encontrar un elemento inverso para esta operacion ⊗:

\displaystyle x \otimes u = \log(u \exp(x)) = x \\ \\ u \log(x) = \log(x) \\ \\ u = 1 (6)

luego la operación ⊗ realizada por la derecha posee el elemento neutro u = 1. Pero, si la realizamos por la izquierda obtenemos:

\displaystyle u \otimes x = \log(x \exp(u)) = x \\ \\ x \log(u) = \log(x) \\ \\ \log(u) = \frac{\log(x)}{x}\\ \\ u = \sqrt[x]{x} (7)

lo cual implica que dicha operación realizada por la izquierda no da un elemento inverso único. Pero, podemos ver cuál sería el opuesto de x (por la derecha):

\displaystyle x \otimes x' = \log(x' \exp(x)) = 1\\ \\ \log(x' \exp(x)) = \log(\exp(0)) \\ \\ x' \exp(x) = \exp(0) \\ \\ x' = \exp(-x) (8)

La infra-potenciación ⊛ puede ser definida así:

\displaystyle x \circledast n = \underset{n}{\underline{x \otimes x \otimes \dots \otimes x}} = \log( \exp(x) x^n) \\ \\ x \circledast n = x + n \log x (9)
Por lo tanto ya estamos en condiciones de representar la función Zeta de Riemann en el inframundo, es decir, de definir uan función que llamaré infra-Zeta de Riemann. Para empezar fijémonis en la clásica forma de la función Zeta de Riemann:

\displaystyle \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} (10)

Expresemos el equivalente a ns en el inframundo así:

\displaystyle n \circledast s = n + s \log n (11)

Ahora presentemos el inverso de dicha infra-potencia:

\displaystyle \exp (-n - s \log n) = \exp (-n) n^{-s} (12)

y realicemos el infra-sumatorio desde n = 1 hasta ∞, para obtener la función infra-zeta de Riemann, \underset{.}{\zeta}:

\displaystyle \underset{.}{\zeta}(s) = \sum_{n=1}^\infty \frac{1}{e^{n} n^s} (13)

Vemos pues que la infra-zeta de Riemann, \underset{.}{\zeta}, es muy parecida a la zeta normal, y la única diferencia visible es que aparece el factor exp(- n), y siempre teniendo en cuenta que el sumatorio son infra-sumas

Saludos

Posted in Matemáticas | Tagged: , , , , , , , , , , , , , , , , , , , , , , | Leave a Comment »

Logaritmos: definición de infrasuma e infrarresta

Posted by Albert Zotkin on August 17, 2014

Hola amigos de Tardígrados. Hoy voy a intentar definir dos nuevas operaciones aritméticas, que llamaré infrasuma e infrarresta. Empecemos. Sabemos que el logaritmo neperiano de un producto de dos números reales es igual a la suma de los logaritmos neperianos de sus factores

\displaystyle \log (a \times b) = \log (a) + \log (b) (1)

y para la división tenemos que

\displaystyle \log \left (\frac{a}{b}\right ) = \log (a) - \log (b) (2)

Siguiendo este proceso operativo, nos podemos preguntar si existe un operador binario ⊕ tal que

\displaystyle \log (a+b) = \log (a) \oplus \log (b) (3)
Por lo tanto, desde el operador binario suma + deberiamos poder definir ese operador binario ⊕ que llamaríamos infrasuma. De igual forma deberíamos poder definir un operador binario ⊖ tal que

\displaystyle \log (a-b) = \log (a) \ominus \log (b) (4)

De hecho es posible expresar esa nuevas operaciones binarias de forma explícita así:

\displaystyle x \oplus y = x+\log \left (1 + \exp (y-x) \right ) \\ \\ x \ominus y = x+\log \left (1 - \exp (y-x) \right ) (5)

La demostración de esto último es fácil, pues sabemos que:

\displaystyle x = \log(a) \ \ \ y = \log(b)

con lo cual tenemos que:

\displaystyle x \oplus y =\log(a) \oplus \log(b) = \log(a+b)= \log(a) +\log \left (1 + \exp (\log(b)-\log(a)) \right ) \\ \\ \log(a+b)= \log(a) +\log \left (1 + \exp (\log\frac{b}{a}) \right ) \\ \\ \log(a+b)= \log(a) +\log \left (1 + \frac{b}{a} \right ) \\ \\ \log(a+b)= \log(a) +\log \left (\frac{a + b}{a} \right ) \\ \\ \log(a+b)= \log(a) +\log (a + b) -\log(a) \\ \\ \log(a+b)= \log (a + b) \\ \\ (6)

La demostración para la infrarresta se hace igual:

\displaystyle x \ominus y =\log(a) \ominus \log(b) = \log(a-b)= \log(a) +\log \left (1 - \exp (\log(b)-\log(a)) \right ) \\ \\ \log(a-b)= \log(a) +\log \left (1 - \exp (\log\frac{b}{a}) \right ) \\ \\ \log(a-b)= \log(a) +\log \left (1 - \frac{b}{a} \right ) \\ \\ \log(a-b)= \log(a) +\log \left (\frac{a - b}{a} \right ) \\ \\ \log(a-b)= \log(a) +\log (a - b) -\log(a) \\ \\ \log(a-b)= \log (a - b) \\ \\ (7)
A continuación se puede comprobar, por ejemplo, si el operador binario infrasuma ⊕ forma un grupo dentro del conjunto de los números reales. Se han de cumplir las siguientes propiedades.

1. Clausura respecto de la infrasuma ⊕: para dos números reales x e y, x⊕y debe ser un número real Comprobamos que para el caso particular x = 0, y = 0, tendriamos,

\displaystyle 0 \oplus 0 =\log(1) \oplus \log(1) = \log(1+1) = \log(2) (8)
El caso por el que la clausura no se cumpliría sería para log(0), pero para que eso ocurriese en una infrasuma debería darse el caso especial exp(y–x) = -1, pero eso caso sólo resultaria cuando:

\displaystyle y - x = n i\pi
siendo n un número entero impar. Es decir, y – x sería un número imaginario puro, pero como x e y son números reales, su resta nunca puede ser un número complejo (imaginario puro).

2. Elemento identidad:

\displaystyle (x \oplus 0) = 0 \oplus x = 0 (9)

Pero, eso no siempre es cierto para todo número real x. Por ejemplo:

\displaystyle (3 \oplus 0) = 3.0485873515737420588\dots
Por lo tanto, ya no sería necesario seguir comprobando si se cumplen las demás propiedades de un grupo, como son la propiedad asociativa y el elemento inverso. La infrasuma no formaría un grupo en el conjunto de los números reales, y tampoco la infrarresta. Pero, estamos buscando un número real y tal que x⊕y = x. Con lo cual, sólo para el caso y = -∞ se cumpliría eso. Pero, -∞ (menos infinito) no es ningún número, por lo tamto la infrasuma no posee elemento identidad.

Supongamos que la infrasuma posee elemento identidad – ∞, entonces podemos seguir viendo si se complen las demás propiedades para formar un grupo. Así, para el elemento inverso hay que ver si x⊕x’ = x’⊕x = – ∞, donde x’ sería el inverso de x. Al resolver esa ecuación obtenemos la solución

\displaystyle x' = x+i\pi (10)

Es decir, el inverso de x no sería un número real sino complejo con parte imaginaria 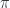\pi.

Saludos

Posted in Matemáticas | Tagged: , , , , , , , , , , , , , , , , , , , | Leave a Comment »