¿Pero, qué diablos es realmente la gravedad? : O ¿por qué la ciencia aceptó las ideas absurdas de Einstein, que desde hace ya más de un siglo nos han llevado a un callejón sin salida, del que sólo se podrá salir definitivamente dentro de mil años o más?

Cuando Albert Einstein se vio en la cima del éxito por su Relatividad General (todos sabemos que Einstein era un genio … un genio del marketing, de la auto promoción, por supuesto), con su vanagloria en alza, y su inmenso ego, más inflado que nunca, allá por los años treinta y pico, en una de las infinitas y cuidadas entrevistas que concedía a los medios, dijo algo asi como: “Newton, perdóname; tú encontraste el único camino que, en tus tiempos, era posible para un hombre de inteligencia y capacidad creadora supremas“. O sea, en su falsa modestia, Einstein nos estaba diciendo que su capacidad creadora e inteligencia eran superiores a las de Newton. La genialidad de Einstein fue que supo vendernos humo, y lo hizo en cantidades industriales.

En cuanto al tema de la gravedad (o gravitación), a estas alturas del siglo XXI, parece ser que Einstein sólo tuvo razón en una cosa al afirmar que la gravedad no era una verdadera fuerza. El problema es que la gravedad tampoco parece ser ya ese efecto de la curvatura del espacio-tiempo, tal como tan bellamente nos lo cantaba el “poema épico” de la Relatividad General con sus matemáticas trileras, elaboradas por prestigiosos masterchefs del axioma, como Hilbert y otros, en más de un siglo de autocomplacencia. Einstein casi tuvo razón en otra cosa, pero al final se retractó, porque el precio mediático a pagar era superior al de la corrección política. Einstein, junto con Nathan Rosen, llegó a afirmar en 1936, sin tapujos, que las ondas gravitacionales no existían. Aunque ese concepto de las ondas gravitationales lo había deducido él mismo de su misma Relatividad General, unos cuanto años antes, al final dio su brazo a torcer, desistió de su “descabellada idea”, porque la presión mediática era inmensa, y su prestigio, su reputación social y académica estaban en juego.

En este pequeño artículo que hoy os presento, veremos qué es realmente la gravedad, y por qué las ondas gravitacinales no pueden existir si la gravedad es lo que aquí voy a afirmar que es.

La gravedad es una fuerza entrópica. Si, ya sé que desde la física oficial, tratan de barrer toda hipótesis que afirme que la gravedad es una fuerza entrópica. Sobre todo, existen infinitos artículos (mainstreamófilcos = muy del consenso oficial) que aparentemente demuestran que la Gravedad Entrópica de Verlinde es inconsistente. El dogma oficial, cuando quiere sofocar algo que incomoda a la doctrina reinante, siempre se basa en demostrar aparentemente que ese algo es inconsistente. El problema es que al final todo se reduce a creer o no que la demostración de la inconsistencia es consistente. La gravedad entrópica de Verlinde, no es toda la verdad sobre la afirmación de que la gravedad es una fuerza entrópica. Los que intentan desacreditar a Verlinde por su teoría entrópica de la gravedad, siempre basan su armas en que dicha teoría posee errores que la reducen a una mera expresión de la teoría clásica de Newton, no ya siquiera a una MOND, y por lo tanto, como la teoría clásica de Newton es incorrecta según el consenso de los mainstreamófilos, porque la correcta es la de Einstein, asi de incorrecta debe ser la de Verlinde . Pero, examinando a fondo esta teoría de la Gravedad Entrópica de Verlinde, se llega a la conclusión de que basicamente es correcta, y en lo único que falla es en la elección de los modelos matemáticos y termodinámicos para deducirla desde primeros principios. En esencia, de lo que carece la Gravedad Entrópica de Verlinde es de la componente gravitomagnética, la cual hay que deducir también desde principios termodinámicos. Eso fue lo que yo hice hace tiempo en mi artículo: Gravedad Cuántica: Análisis pormenorizado de la componente entrópica de la gravedad. Pero veamos sucintamente en que consiste la Gravedad Entrópica de Verlinde, y por qué la atacaban tan furibondamente desde el consenso de los mainstreamófilos.

A estas alturas del siglo XXI, aún se pueden leer blogs de ciencia, donde supuestos científicos (y científicas) hacen afirmaciones sobre agujeros negros (hipotéticos objetos, de cuya existencia no tendremos nunca una prueba definitiva) tales como: “Dos agujeros negros uniéndose no emiten radiación electromagnética, porque los agujeros negros no están hechos de materia que pueda emitir esa clase de radiación. Pueden estar rodeados de materia que sí la emite, pero es demasiado pequeña para ser observada.” Es decir, siguen tratando el espacio-tiempo como si fuera una sustancia, una especie de éter flexible que pueda ser estirado, retorcido o curvado. Que yo sepa, el espacio-tiempo no existe físicamente hasta que no se demuestre experimentalmente por separado que el espacio existe y que el tiempo existe. Pero mucho me temo que ambas entidades que tanto se emplean en física, son más axiomas o postulados que algo real existente en la naturaleza.

Hace ya algún tiempo un tal Erik Verlinde publicó un artículo en el que supuestamente deducía la ley de gravitación universal de Newton desde primeros principios, incluso dedujo las ecuaciones de campo de Einstein de la Relatividad General, concluyendo que la gravedad es una fuerza entrópica, es decir una fuerza que no es fundamental y que emerge naturalmente del aumento de entropía de los sistemas materiales. Verlinde usó el principio holográfico y las conocidas leyes de la termodinámica, junto con algunas cosillas más, para deducir dicha fuerza entrópica. Las fuerzas entrópicas emergen desde el microcosmos hacia el macrocosmos debido a que los sistemas materiales tienden a adoptar estados de máxima entropia. Cuando estiras una goma elástica debes de ejercer una fuerza para contrarrestar temporalmente su estado maximizado de entropía. Al estirar la goma estás rebajando su entropia, y por lo tanto la goma se opone a ese cambio ejerciendo una fuerza en sentido contrario que intenta restaurar su estado de máxima entropía.

Pero, como vamos a ver ahora, esa fuerza entrópica deducida por Verlinde desde primeros principios, y que emerge siendo la fuerza de gravitación de Newton, es sólo una componente de la gravedad total. En concreto vamos a ver cómo esa componente entrópica es engullida brutalmente por un tiburón cuántico que habita en las profundidades del microcosmos termodinámico.

Comencemos expresando la Primera Ley de la Termodinámica para sistemas homogeneos cerrados:

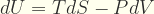(1)

donde dU es el cambio de energía interna, T es la temperatura, dV es el cambio de volumen, dS es el cambio de entropia, y P es la presión. Sabemos que PdV es el cambio de energía libre del sistema, por lo tanto puede ser expresada como suma de los cambios de energía de cada uno de los microestados

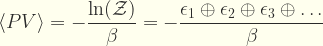(2)

Donde e_s representa la energía del microestado s, Z es la función de partición, y β es menos el inverso del producto de la temperatura por la constante de Boltzmann:

La ecuación (1) para un proceso con presión y temperatura constantes queda así:

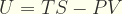(3)

por lo tanto sustituyendo (2) en (3) tenemos:

(4)

Según el postulado fundamental de la mecánica estadística, la entropía S es directamente proporcional al logaritmo del número Ω de microestados:

es decir

(5)

por lo que (4) lo podemos calcular más fácilmente:

(6)

Esta energía interna U es lo que en gravedad debe identificarse como la energía potencial gravitatoria, la cual si es dividida por la masa m de una partícula de prueba tendremos el potencial gravitatorio (con todas sus componentes) en el punto espacial donde está localizada dicha partícula:

(7)

Recapitulemos. La componente entrópica debe ser identificada con la gravitación clásica de Newton, y la componente de energía libre (PV) debe ser identificada con lo que se llama gravitomagnetismo. O lo que es lo mismo, la función de partición Z mapea dicho gravitomagnetismo, mientras que el número Ω de microestados mapea la componente estática de gravitación Newtoniana.

Pongamos un pequeño ejemplo. Supongamos que queremos calcular el número Ω de microestados de un sistema gravitatorio binario, con masas M y m. Igualamos el potencial gravitatorio así:

pero en β está incluida la temperatura T, por lo tanto si igualamos esa temperatura con la temperatura de Unhru: ,

y la aceleración a la igualamos a la aceleración del campo gravitatorio estático, a = g:

Por lo que el número Ω de microestados para ese sistema gravitatorio será:

Las fuerzas entrópicas están muy relacionadas con los paseos aleatorios

y por lo tanto, la gravedad es una interacción estrechamente relacionada con lo que se llama paseos aleatorios de máxima entropía.

Distancia al centro del universo. El tamaño del presente: ¿Por qué parece imposible superar la velocidad de la luz en el vacío, y por qué esa velocidad parece ser una constante universal aunque no lo sea?

La velocidad de la luz en el vacío es c = 299.792.458 m/s, la cual nos llevaría a las inmediaciones de la Luna desde la superficie terrestre en menos de 1 segundo. Dicen que dicha velocidad es una constante universal, y que además de ser constante no puede ser superada independientemente del sistema de referencia desde el que se considere. Pero, si tenemos en cuenta las inmensas escalas de espacio y tiempo de nuestro universo observable, esa supuesta constante universal resulta insufriblemente lenta. Para que un rayo laser pudiera atravesar el diámetro de nuestra galaxia, la Vía Láctea, se necesitarían más de cien mil años. Está claro que las ondas electromagnéticas no son el vehículo idóneo para comunicarnos a escalas intergalácticas. De hecho hay fuerzas titánicas, que la naturaleza puede desatar, que podrían, al menos teóricamente, impulsar partículas a velocidades superlumínicas (pero, la Dirección General de Tráfico, que algunos llaman Relatividad Especial, nos prohíbe viajar a más de 299.792.458 m/s por autopistas intergalácticas 😛 ).

Hace 65 millones de años, según cierta teoría, de la que parece que se están acumulando las evidencias a favor, los dinosaurios se extinguieron debido a que un meteorito de 15 kilómetros de ancho chocó contra la Tierra. Para saber si eso fue exactamente así, alguien podría sugerirnos lo siguiente: “bastaría viajar por el espacio a una velocidad superior a la de la luz hasta llegar a un punto clave situado a más de 65 millones de años-luz de la Tierra, y observar con un potente telescopio nuestro planeta. Es decir, estaríamos observando un evento muy remoto del pasado terrestre. Eso deberia ser así porque los fotones de la colisión del meteorito con la Tierra aún no habrían llegado a ese punto clave donde colocamos nuestro telescopio. Es decir, esos fotones aun no han sido absorbidos. Pero, ¿estamos seguros de que eso sería así?. Si viajamos al doble de la velocidad de la luz (v = 2c), nuestro punto clave para observar un evento de nuestro pasado de hace 65 millones de años, estaría exactamente a 130 millones de años-luz. Si viajamos a n veces la velocidad de la luz, nuestro punto clave estaría a 65 millones de años-luz más 65/(n-1) millones de años-luz. En general, para observar un evento que ocurrió hace un tiempo t, habría que viajar a un punto clave x a una velocidad de v = nc, tal que

y la observación del evento sería inmediata, es decir, no tendríamos que esperar a que ocurriera. Si quisiéramos esperar cierto intervalo de tiempo Δt a que ocurriera el evento, tendríamos que incrementar la localización x a otra más distante x‘, o incrementar nuestra velocidad superlumínica:

Pero, ¿estamos seguros de que fotones que fueron emitidos hace 65 millones de años, desde la Tierra, aún siguen por ahí revoloteando, esperando ser absorbidos por algún sistema material?. ¿Y si resulta que es imposible superar la velocidad de la luz c en el vacío por la sencilla razón de que el fotón emitido fue instantaneamente absordbido por algún sistema material, independientemente de la distancia que separó al emisor del receptor?. La hipótesis que planteo es simple. Existiría un desfase de tiempos presentes entre dos sistemas materiales distantes. Si Alicia está separada de Bob por una distancia x constante, entonces sus tiempos presentes están desfasados un intervalos Δt = x/c. Ese desfase es relativo, y significa que el presente del sistema remoto está siempre en algún tiempo pasado del sistema material localizado en el origen de nuestro sistema de referencia.

“Tu presente está en mi pasado, y en tu pasado está mi presente, porque entre tú y yo existe la distancia“.

De esta forma tan poética, eliminamos las paradojas de la Relatividad Especial de Einstein. La luz no viaja, simplemente permanece estacionaria, hasta que el fotón es eventualmente alcanzado por un sistema material anclado en una expansión concéntrica relativa.