La reflexión de un rayo de luz en un espejo móvil falsaría la Relatividad Especial

Una fuente de luz y un observador están en reposo en el mismo sistema inercial de referencia, donde r es el vector distancia entre ellos. Un espejo, que se mueve alejándose de ellos perpendicularmente a r por el punto medio, está ahora a una altura h, llevando una velocidad u y refleja luz de la fuente hacia el observador. Podemos conocer las componentes de velocidad v₁ y v₂ con respecto a la fuente y al observador respectivamente. Esas componentes de velocidad poseen la misma magnitud, v, asi que podemos escribir

Y en ángulo entre y es

por lo tanto,

El observador detecta el rayo reflejado como si procediera de la imagen tras el espejo. Puesto que el espejo se mueve con velocidad v₁ con respecto a la fuente de luz y con v₂ respecto al observador, crea una imagen virtual de la fuente de luz alejándose con una velocidad de w = 2v a lo largo de la linea de vista,

Entonces, para esa velocidad virtual w, la cual puede incluso ser superluminal, porque no corresponde a ningún movimiento real entre fuente de luz y observador (recordemos que fuente de luz y observador están en reposo), podemos predecir una frecuencia Doppler observada desplazada hacia el rojo de la frecuencia original f₀,

*Apéndice: Desde un contexto de la Relatividad Especial, la predicción sería como sigue. Aplica una adición de velocidades de Einstein,

Ahora aplica un Doppler relativista, así

Y después de un poco de álgebra, sabiendo que , se obtiene que

¿Dónde está el error engañoso en esta derivación?. Podemos ver que hay dos nociones erróneas, las cuales cuando actuan de forma cooperativa, intentan ligéramente compesar la respuesta errónea originando una medianamente decente. El primer error consiste en asumir que debe existir la siguiente adición relativista de las velocidades, w = 2v/(1 + v²/c²). Eso no tiene mucho sentido, es absurdo, ya que w es una velocidad VIRTUAL de la fuente de luz con respecto al observador (pero ambos están en reposo), no una velocidad real (esta puede ser incluso superluminal), una adición relativista de velocidades NO procede ser aplicada en tal caso. Si la w es superluminal , significa que, una vez que el observador detecta el rayo de luz como procedente de la imagen virtual tras el espejo, la información no es más rápida que la luz porque esa información ha viajado en realidad una trayectoria más larga que la de una linea recta desde la fuente de luz al observador, por lo tanto esa información viajó con la luz, no es superluminal. Este error de concepto que se comete en la relatividad especial es después ligeramente corregido cuando se aplica el Doppler relativista a f₀ através de esa errónea w, obteniendose una predicción de frecuencia f’ que está muy próxima a la correcta f, que se ha ofrecido arriba. En realidad, f/f₀ y f’/f₀ sólo empiezan a diferir desde el tercer orden de sus respectivas series de potencias,

El número π (PI) visto desde una n-bola

Materia Oscura: Mi hipótesis, que ahonda en la ruptura espontánea de simetría como modelo

¿Qué es la materia oscura?. ¿Por qué los modelos actuales no son capaces de describir correctamente lo observado?. La materia oscura es una anomalía astrofísica. Una anomalía es una discrepancia entre la teoría y la observación, lo cual en negativo, puede indicar tres cosas, que la teoría no es correcta, que no sea correcta la observación, o que no sean correctas ambas. Aquí supondremos que la observación es correcta, y lo que se observa es que la mayoría de las galaxias y cúmulos de galaxias giran alrededor de sus respectivos centros más rápido de lo esperado. O más exactamente, sus rotaciones se comportan como si fueran las de discos compactos rígidos, más que si fueran fluidos.

En este breve artículo explicaré qué es, en mi opinión, la materia oscura, cómo se forma, y qué efectos observables presenta.

Imaginemos una playa bastante grande y plana, llena de fina arena. Unos niños juegan en ella, y hacen un bonito castillo de arena.

El proceso por el que esos niños han construido el castillo de arena es simple: Primero amontonan arena, formando un buen montón de arena húmeda, que no se desmorone fácilmente. Evidentemente, la arena no la han traído de otro lugar, sino que es la arena que se encuentra en ese mismo sitio, pero amontonada en cierta cantidad. ¿Qué ocurre?. Pues ocurre que al amontonar arena, los niños han creado un pequeño foso alrededor del montón. La arena que hay de más en el montón es precisamente la que falta alrededor. Eso, que parece tan obvio, no son capaces de verlo los científicos y astrofísicos actuales. Estos sabios astrónomos se lían tanto con sus difíciles y engorrosas teorías que no son capaces de ver lo obvio, el bosque. Los árboles de su corta visión les impide ver el bosque. Y el bosque es simple. Cuando la gravedad amontona materia para la formación de una galaxia, no trae materia de muy lejos, sino que es precisamente la materia local la utilizada. Una galaxia no es más que un montón de arena en una playa casi infinita y muy plana. ¿Qué ocurre a ese montón de materia que llamamos una galaxia?. Pues ocurre que alrededor de ella queda un foso, un “anti-montón” de materia. ¿Qué significa eso?. Significa que si la media de densidad de materia entre estrellas de una galaxia es de 0.1 átomos de hidrógeno por centímetro cúbico, en uno de esos fosos gravitacionales el promedio será significativamente menor. Eso, traducido al terreno del potencial gravitatorio implica que existe realmente una modificación de la Ley de Gravitación Universal de Newton. Un típico potencial clásico (de Newton), es simplemente una ley del inverso de la distancia:

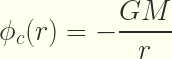
Pero, esa ley de gravitación no explica, en su sencillo potencial, el comportamiento anómalo de la rotación de las estrellas en las galaxias, ni de las galaxias en cúmulos. ¿Qué ocurre?. ¿Es la Ley de Gravitación Universal incorrecta?. El señor Einstein se apresuró hace más de cien años a decir que sí, que la Ley de Newton es incorrecta, que le perdonásemos a él, el señor Einstein, por enmendar a un gigante como Newton, al proponer su Relatividad General. Pero, resulta que la Relatividad General de Einstein tampoco es capaz de explicar, ni predecir esa anomalía que llamamos materia oscura. Aquí vamos a ver, por qué todo esto falla. Dejando a parte la Relatividad General, y usando sólo la aparentemente sencilla ley de gravitación de Newton, veremos cómo debe ser el potencial de un sistema galáctico, donde entran en juegos miles de millones de masas solares. El potencial Newtoniano indicado arriba, nos da una grafica en función de la masa M de la galaxia, y su distancia r al baricentro, como la siguiente:

La linea amarilla representa el nivel cero de potencial, el cual nunca se alcanza, ni siquiera en una distancia r infinita. Es decir, que todos los valores reales de potencial son negativos, para un potencial Newtoniano. Pero, ahora vamos a considerar el potencial modificado, de tal forma que esa función φ ya no será exactamente una ley del inverso de la distancia. Y su representación gráfica será algo más compleja:

Aquí vemos que parte de la curva ha traspasado la linea amarilla de potencial cero, para formar un “anti-montón”, un foso gravitacional, que tendrá un valle (concavidad) finito, pero que recupera su tendencia a aproximarse al potencial cero con la distancia. Eso significa que si la linea amarilla representa espacio donde la densidad de materia bariónica es en promedio 0.1 átomos de hidrógeno por centímetro cúbico, entonces la parte de la curva que está por encima de esa línea amarilla representa espacio donde la densidad de materia es menor a ese promedio. Esa es la materia oscura: vacío cósmico donde la densidad de materia bariónica es significativamente menor al valor promedio para el se que se define un potencial gravitatorio igual a cero.

Si ampliamos la escala de la gráfica del nuevo potencial, vemos que la curva vuelve a ser asintótica, pero ahora desde valores de potencial positivos, hacia la linea amarilla de potencial cero:

Podemos explicitar esa curva de potencial gravitatorio, como un potencial newtoniano modificado, y su función sería exactamente una Onda de Ricker:

Donde σ es la desviación media. Esto indica también, que este potencial gravitatorio está relacionado con la viscosidad newtoniana, ya que la onda de Ricker es una solución a las ecuaciones diferenciales de navier-stokes y que fue propuesta por Ricker en el año 1943.

Pero, ¿por qué este nuevo potencial gravitatorio puede explicar la anomalía de la materia oscura?. Lo explica por la sencilla razón de que no existen masas negativas. Las masas son siempre de un único signo, y siempre se atraen. Por lo tanto, al existir potencial por encima de la linea de potencial cero, esas zonas se comportan como si fueran masa extra, aunque sólo es vacío con densidad de materia muy por debajo del promedio que marca la linea amarilla. Lo cual significa que el vacío también atrae, como si fuera una masa. De hecho las masas tienden a atraerse porque existe un vació entre ellas que es mayor que el vacío exterior a ellas. Un gas se expande siempre hacia las zonas de menor densidad, nunca al contrario.

Pongamos ahora una masa de pruebas en la cúspide entre el foso y el potencial del sistema gravitatorio en cuestión. Esa masa quedará en equilibrio inestable, pudiendo caer hacia el baricentro del sistema o hacia el foso. En eso consiste la ruptura espontánea de simetría.

¿por qué algunas galaxias y cúmulos no presentan cantidades significativas de materia oscura, y otras sí, si parecen ser de tamaños muy parecidos?. Cuando una galaxia, o un cúmulo de galaxias, se forma muy lentamente, en comparación con el tiempo medio de formación, lo que llamamos materia oscura, y que aquí yo llamo foso gravitatorio, no llega a tener mucha significación. Si hablamos de foso diremos en ese caso que la profundidad del foso gravitatorio de una galaxia que se ha formado muy lentamente es poco profundo o inexistente. Esto indica, que a la inversa, esta hipótesis predice que la materia oscura se evapora. Un foso muy pronunciado, porque la galaxia se formó muy rápidamente, acabará deshaciéndose, porque la materia poco a poco se irá dispersando, cayendo hacia el foso, ya sea desde fuera del sistema o desde dentro.

¿Cuanto tiempo sería necesario para que una galaxia o un cúmulo de galaxias evaporara toda su materia oscura, o lo que es lo mismo, para que el foso gravitatorio se deshiciera?. Dependería de muchos factores, pero grosso modo, podemos decir que necesitaría el mismo tiempo que empleó para su formación.

Pongamos algún ejemplo. La galaxia NGC 1052-DF2 posee muy poca materia oscura o ninguna. Eso, según mi hipótesis, indica que es una galaxia muy antigua, con una edad aproximada del doble de la edad de las galaxias promedio de su tamaño y forma que sí muestran materia oscura.

Esa galaxia sería tan antigua, ya sea porque se formó muy lentamente, y por lo tanto no formó foso, o ya sea porque se formó en un tiempo estándar, como cualquier otra galaxia media, pero su foso se deshizo poco a poco al cabo de un tiempo aproximadamente igual al de su formación. En cualquiera de los dos casos, esa galaxia tiene doble edad que las galaxia que sí exhiben materia oscura.

Y hasta aquí llegó el post de hoy.

Saludos

¿Existe Dios?: La sucesión de números primos Catalan-Mersenne

Eugène Charles Catalan se dió cuenta de que, en la sucesión de números Mersenne, los siguientes términos

eran todos números primos. Por lo tanto, la sucesión de números definida de esa forma:

con

son conocidos como Números Catalan-Mersenne.

No se sabe si el término

es o no primo. De él lo único que se sabe es que no tiene factores primos menores que 10⁵¹ . En general, de esta clase de números, lo que sí sabemos seguro es que si un número Catalan-Mersenne

es primo, entonces todos sus predecesores

son primos también. Y si ese mismo número no es primo entonces todos sus infinitos sucesores

tampoco serían primos. Eso significa que en la sucesión infinita de Números Catalan-Mersenne, existiría un último número primo, a partir del cual los infinitos siguientes números serían números compuestos, o podría no existir ninguno. Al inmediato sucesor de ese supuesto último número primo de la sucesión Catalan-Mersenne lo llamaré Dios. ¿Existe Dios?, o ¿son todos los números de la sucesión infinita números primos?.

Representemos esos números Catalan-Mersenne con esferas coloreadas, atendiendo a cierto código de color, así tendremos una visión más clara de esa clase de números:

Criptografía: un programilla muy sencillo más para codificar cadenas

Hace ya algunos años, escribí y compilé un pequeño programa en lenguaje C para encriptar archivos. Era simple y directo. Ahora, lo he rescatado y lo he traducido a lenguaje javascript para node.js. Y aquí te lo presento:

/*
 ESTE PEQUEÑO PROGRAMILLA HACE LO SIGUIENTE:
 			1. DIVIDE LA CADENA DE BYTES EN DOS MITADES. DESPOUES, 
 			2. TRASPONE EL BYTE DE LA POSICIÓN X A LA POSICIÓN 
 				 L - X, DONDE L ES LA LONGITUD DE LA CADENA. Y SEGUIDAMENTE 
 				 
 			3. RESTA(Ó SUMA, DEPENDIENDO DE SI EL PARÁMETRO MODO ES 1 Ó 0) 
 				 AL CÓDIGO ASCII DE CADA BYTE.
*/

const fs = require('fs');
var file1 = '../uploads/building.jpg';
var file2 = '../uploads/building-2.jpg';
var flujofichero = fs.readFileSync(file1);
var puntero = 0;
var modo = 1;
var size = flujofichero.length;

if(flujofichero.length){
 while(puntero < size/2)
  {
    Traspuesta(puntero,size-puntero-1,modo,flujofichero);
    puntero++;   
  }
 
  fs.writeFile(file2, flujofichero, 'binary', function(err){ 	
  });
}




function Traspuesta(i, j, modo, buffer){ 

  var nparam1,nparam2;
  nparam1 = buffer.readUInt8(i);
  if(modo)nparam1 = nparam1 - 10;
  else nparam1 = nparam1 + 10;
  nparam1 = nparam1<0?256+nparam1:nparam1;
	nparam1 = nparam1>0xff?nparam1-256:nparam1;
  nparam2 = buffer.readUInt8(j);//flujofichero.charCodeAt(j);
  if(modo)nparam2 = nparam2 - 10;
  else nparam2 = nparam2 + 10;
 
  nparam2 = nparam2<0?256+nparam2:nparam2;
	nparam2 = nparam2>0xff?nparam2-256:nparam2;
  buffer.writeUInt8(nparam2, i);
  buffer.writeUInt8(nparam1, j);
}

En el código de arriba elijo un archivo de una imagen jpg llamado building.jpg. Lo abro mediante la instrucción flujofichero = fs.readFileSync(file1);, con lo cual sus bytes quedan cargados en la variable flujofichero , que es un buffer. Conprobamos que dicho buffer tiene longitud no nula, antes de aplicarle el proceso de encriptación. Resulta que nuestro archivo imagen posee una longitud en bytes de flujofichero.length = 699.395 bytes.

Ahora ya podemos empezar a encriptar. Aplicamos la función Traspuesta a lo largo de la cadena de bytes, y eso lo hacemos mediante un loop while, con la condición de que salga del bucle cuando la variable puntero sea igual o mayor a la mitad de la longitud de la cadena de bytes. La función Traspuesta es muy sencilla, el único misterio está en cono se puede truncar cada bytes al restarle o sumarle 10. Cuando a 1 byte, cuyo valor sabemos que está en el intervalo [0,255], porque 1 byte son 8 bits, le sumamos un número tal que el resultado desbordaría esos 8 bits, es decier se necesitarían más bits para expresar el resultado, entonces se produce un truncamiento. Pero ese truncamiento del byte Javascript no es posible porque las variables de javascript no poseen esa pre-condición. Por lo tanto, el truncamiento del byte hay que hacerlo manualmente. ¿Cómo?. Muy sencillo. Supongamos que tenemos el byte almacenado en la variable nparam1 y al sumarle 10 se desborda, entonces le aplicamos la siguiente condición, en caso de que se produzca ese desbordamiento:

nparam1 = nparam1>0xff?nparam1-256:nparam1;

que viene a decir que en caso de que la variable nparam1 sea mayor a 255, entonces quede truncada a nparam1-256. Algo muy parecido hacemos para el caso en que la variable sea un número negativo

 nparam1 = nparam1<0?256+nparam1:nparam1;

De esta forma el byte queda truncado, siempre tendremos 8 bits, y por lo tanto el tamaño del archivo encriptado será el mismo que el del original. Estos truncamientos se pueden hacer de muchas formas, yo he elegido la más “literaria”. El resultado de encriptar lo guardamos en otro archivo nuevo llamado building-2.jpg, y eso lo hacemos mediante la función asincrónica

 fs.writeFile(file2, flujofichero, 'binary', function(err)
{if(err)throw err;});

Otra cosa interesante de este programilla de encriptar es el parámetro modo. Si encriptas en modo = 1, entonces para recuperar el archivo original debes aplicar una encriptación sobre el archivo encriptado, pero con modo = 0. y viceversa. Si aplicas sucesivas iteraciones con el mismo modo, solo al cabo de 128 iteraciones consigues llegar al archivo original.

Veamos el aspecto de los dos archivos, el original y el encriptado:
y los primeros bytes de esa imagen original son estos:

00000000h: FF D8 FF E0 00 10 4A 46 49 46 00 01 02 01 00 48 ; ÿØÿà..JFIF.....H
00000010h: 00 48 00 00 FF E1 29 8A 45 78 69 66 00 00 4D 4D ; .H..ÿá)ŠExif..MM
00000020h: 00 2A 00 00 00 08 00 07 01 12 00 03 00 00 00 01 ; .*..............
00000030h: 00 01 00 00 01 1A 00 05 00 00 00 01 00 00 00 62 ; ...............b
00000040h: 01 1B 00 05 00 00 00 01 00 00 00 6A 01 28 00 03 ; ...........j.(..
00000050h: 00 00 00 01 00 02 00 00 01 31 00 02 00 00 00 1C ; .........1......
00000060h: 00 00 00 72 01 32 00 02 00 00 00 14 00 00 00 8E ; ...r.2.........Ž
00000070h: 87 69 00 04 00 00 00 01 00 00 00 A4 00 00 00 D0 ; ‡i.........¤...Ð
00000080h: 00 0A FC 80 00 00 27 10 00 0A FC 80 00 00 27 10 ; ..ü€..'...ü€..'.
00000090h: 41 64 6F 62 65 20 50 68 6F 74 6F 73 68 6F 70 20 ; Adobe Photoshop 
000000a0h: 43 53 34 20 57 69 6E 64 6F 77 73 00 32 30 31 37 ; CS4 Windows.2017
000000b0h: 3A 30 33 3A 30 31 20 32 32 3A 32 38 3A 32 32 00 ; :03:01 22:28:22.
000000c0h: 00 00 00 03 A0 01 00 03 00 00 00 01 00 01 00 00 ; .... ...........
000000d0h: A0 02 00 04 00 00 00 01 00 00 03 69 A0 03 00 04 ;  ..........i ...
000000e0h: 00 00 00 01 00 00 02 D9 00 00 00 00 00 00 00 06 ; .......Ù........
000000f0h: 01 03 00 03 00 00 00 01 00 06 00 00 01 1A 00 05 ; ................
00000100h: 00 00 00 01 00 00 01 1E 01 1B 00 05 00 00 00 01 ; ................

L Y los primeros bytes del archivo encriptado en mod = 0, son estos:

00000000h: E3 09 49 F5 89 8D 3B 06 D1 0F 94 0A 09 F9 F4 29 ; ã.Iõ‰;.Ñ.”..ùô)
00000010h: C1 FC C9 6E AA 02 C9 9C F5 11 4D 02 E9 94 1D 0A ; ÁüÉnª.Éœõ.M.é”..
00000020h: 09 E9 62 71 90 FC A9 EB E0 0A 09 AD D8 55 D4 0A ; .ébqü©ëà..­ØUÔ.
00000030h: 09 5C CE 89 DC 7F 19 06 61 43 98 0A 09 48 B8 81 ; .\ΉÜ..aC˜..H¸
00000040h: 06 D3 89 61 00 81 62 A1 3F EA 0A 09 E9 05 A1 7B ; .Ó‰a.b¡?ê..é.¡{
00000050h: 27 01 CC 0A 09 FC 04 49 B4 95 0F 0A 09 75 EB 05 ; '.Ì..ü.I´•...uë.
00000060h: C9 62 39 FC BD 0A 09 45 70 07 19 F4 1A A1 07 E9 ; Éb9ü½..Ep..ô.¡.é
00000070h: 3A 21 0A 09 87 7F 2B 19 02 C9 EE 35 08 2D B6 A9 ; :!..‡+..Éî5.-¶©
00000080h: 28 FC E9 EF 35 08 41 87 C2 D3 0A 09 9F 8F 02 0A ; (üéï5.A‡ÂÓ..Ÿ..
00000090h: 09 BC 78 44 06 79 ED 07 95 F4 30 9B 0A 09 62 98 ; .¼xD.yí.•ô0›..b˜
000000a0h: F7 0A 09 AE D8 B4 EB C9 FB C6 89 9F 7F A3 5F 03 ; ÷..®Ø´ëÉûƉŸ£_.
000000b0h: 39 D2 02 59 B4 95 11 0A 09 67 C5 07 D9 7E 6B CD ; 9Ò.Y´•...gÅ.Ù~kÍ
000000c0h: 0A 09 D5 A1 02 89 B8 98 1E 02 29 62 CE 0A 09 63 ; ..Õ¡.‰¸˜..)bÎ..c
000000d0h: 47 B2 4E 0A 09 19 7F F9 89 B3 19 E6 D3 0A 09 5C ; G²N...ù‰³.æÓ..\
000000e0h: 02 08 7B E0 65 13 08 B9 03 96 0A 09 BE C4 94 C1 ; ..{àe..¹.–..¾Ä”Á
000000f0h: FC C9 BF E5 0A 09 11 F5 D6 5F 08 ED DC 01 79 BD ; üÉ¿å...õÖ_.íÜ.y½
00000100h: 18 D6 08 39 3F F9 C9 B2 FD C8 01 89 FA 08 65 E0 ; .Ö.9?ùɲýÈ.‰ú.eà

Como me pareció un script muy sencillo y útil, lo he incluido como función dentro de mi libreria de utilidades de node.js, para cuando necesite una sencilla e inmediata encriptación de algo.

'use strict';
const OUTPUT = 1;
const INPUT = 0;
function WM_Encrypt(buffer, mode){
		 if(buffer.length){
				var puntero = 0;
				var size = buffer.length;
 				while(puntero < size/2)
  					{
    					Traspuesta(puntero,size-puntero-1,mode,buffer);
    					puntero++;   
  					}
		}
		
		return buffer;
}
function Traspuesta(i, j, modo, buffer){ 

  var nparam1,nparam2;
  nparam1 = buffer.readUInt8(i);
  if(modo)nparam1 = nparam1 - 10;
  else nparam1 = nparam1 + 10;
  nparam1 = nparam1<0?256+nparam1:nparam1;
	nparam1 = nparam1>0xff?nparam1-256:nparam1;
  nparam2 = buffer.readUInt8(j);//flujofichero.charCodeAt(j);
  if(modo)nparam2 = nparam2 - 10;
  else nparam2 = nparam2 + 10;
 
  nparam2 = nparam2<0?256+nparam2:nparam2;
	nparam2 = nparam2>0xff?nparam2-256:nparam2;
  buffer.writeUInt8(nparam2, i);
  buffer.writeUInt8(nparam1, j);
}

function wm_encode(buffer){
	return WM_Encrypt(buffer, OUTPUT);
}
function wm_decode(buffer){
	return WM_Encrypt(buffer, INPUT);
}
module.exports =
{
	WM_Encrypt:WM_Encrypt,
	wm_encode:wm_encode,
	wm_decode:wm_decode
};

Así, os puedo decir que:

#0ieZejW&eZecd[ieZWjf_hYd[ieZkbWI

que al desencriptarlo en modo 1, ya que fue encriptado en modo 0, obtenemos la cadena:

Saludos encriptados en modo 0 a todos 🙂

Iconos para bloques en la blockchain de bitcoin

Ayer, mientras ganaba algunos miles de euros minando bitcoins, se me ocurrió una idea gráfica, para identificar mediante una imagen a cada uno de los bloques en la blockchain.

Como cada bloque posee tres hashes principales de 32 bytes cada uno: el hash propio del bloque, el del bloque inmediato anterior, y el de la raíz del árbol Merkle de las transacciones., se me ocurrió lo siguiente: cada dígito de cada uno de esos tres hashes podría ser un código de color de una terna RGB, rojo, verde y azul, para cada pixel de la imagen. Pongamos un ejemplo. Elijamos el Bloque Génesis, es decir, el primer bloque de bitcoin que fue minado por el propio Satoshi Nakamoto. El objeto JSON de este histórico bloque es:

{
        "0": {
                "hash": "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
                "version": 1,
                "previous_block": "0000000000000000000000000000000000000000000000000000000000000000",
                "merkle_root": "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
                "time": 1231006505,
                "bits": 486604799,
                "fee": "0.00000000",
                "nonce": 2083236893,
                "n_tx": 1,
                "size": 285,
                "block_index": 0,
                "main_chain": true,
                "height": 0,
                "received_time": null,
                "relayed_by": null,
                "transactions": [
                        {
                                "double_spend": false,
                                "block_height": null,
                                "time": 1231006505,
                                "lock_time": 0,
                                "relayed_by": "0.0.0.0",
                                "hash": "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",
                                "tx_index": 0,
                                "version": 1,
                                "size": 204,
                                "inputs": [
                                        {
                                                "sequence": 4294967295,
                                                "script_sig": "04ffff001d0104455468652054696d65732030332f4a616e2f32303039204368616e63656c6c6f72206f6e206272696e6b206f66207365636f6e64206261696c6f757420666f722062616e6b73",
                                                "coinbase": true
                                        }
                                ],
                                "outputs": [
                                        {
                                                "n": 0,
                                                "value": "50.00000000",
                                                "address": "1A1zP1eP5QGefi2DMPTfTL5SLmv7DivfNa",
                                                "tx_index": 0,
                                                "script": "4104678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5fac",
                                                "spent": false
                                        }
                                ]
                        }
                ]
        }
}

Por lo tanto vemos que los tres hashes principales son:

                "hash": "000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f",
                "previous_block": "0000000000000000000000000000000000000000000000000000000000000000",
                "merkle_root": "4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b",

los cuales son números de 64 dígitos en base hexadecimal, es decir, 32 bytes cada uno. Podemos diseñar una imagen en formato PNG de 64 x 64 pixels. Para ello vamos seleccionado ternas de dígitos para componer el RGB de cada pixel. Así tendremos que el primer pixel de nuestra imagen (posición superior izquierda será el RGB(4,0,0), porque 4 es el primer dígito en el hash de la Merkle root, y 0 para los otros dos. El siguiente pixel sería RGB(a,0,0), y los cuatro siguientes son RGB(5,0,0), RGB(e,0,0), RGB(1,0,0). Pero como esos dígitos son hexadecimales, sólo van desde el 0 al 15, en lugar de ir del 0 al 255, lo cual produciría un color bastante oscuro. Por lo tanto, le vamos a dar brillo a cada pixel duplicando cada componente RGB hasta completar el byte, es decir, sería como multiplicar por 17 cada componente (dígito hexadecimal). Así nuestros pixeles, con brillo serían: RGB(44,0,0), RGB(aa,0,0), RGB(55,0,0), RGB(ee,0,0), RGB(11,0,0), y el ultimo pixel de la imagen PNG sería el RGB(bb, 0, ff). Es decir, nuestra imagen PNG para el Bloque Génesis sería esta:

ID imagen del Bloque Génesis de Satoshi Nakamoto

O sea, podemos crear la imagen dinámicamente mediante lenguaje PHP, creando una función que tome como argumentos esos tres hashes del bloque en un array. Yo escribí el código para una función que haga eso. Esa función es la siguiente:

function ImageFromHash3($hash){
if(strlen($hash[0])!=64 && strlen($hash[1])!=64 && strlen($hash[2])!=64) return '';
// Create a 64 x 64 image
$image = imagecreatetruecolor(64, 64);
$n=0;
$r = str_split($hash[0],1);
$g = str_split($hash[1],1);
$b = str_split($hash[2],1);
				
for ($y = 0; $y < 64; $y+=8){
for ($x = 0; $x < 64; $x+=8) {						
imagefilledrectangle($image, $x, $y, $x+8, $y+8, 
imagecolorallocate($image, hexdec($r[$n])*17, hexdec($g[$n])*17, hexdec($b[$n])*17 ));			   		
$n ++;			
}				 
ob_start();
imagepng($image);
$im = ob_get_contents();
ob_end_clean();
imagedestroy($image);
return '<img src="data:image/png;base64,'.base64_encode($im).'" />';					
}

Y así, la podemos presentar en nuestra página web. Pongamos un ejemplo más. El ultimo bloque validado por la minería de bitcoin, hasta la fecha, tiene una altura de 619122 (la altura n de un bloque significa el orden, o sea, que existen n bloques antes que él en la blockchain). Este bloque de fecha 26/2/2020 22:16:32, posee los siguientes tres hashes:

                "hash": "0000000000000000001159ec899185ec8f056b7655bf7898fef186454efde94f",
                "previous_block": "00000000000000000008e901529a41ef9350ff42166c8abeea80f6e708a46463",
                "merkle_root": "1adeb8334f75e32a335b19005871b2be3ac5555c661ce17b81131b0c43579a61",

y ha sido minado por la pool ViaBTC. La imagen generada con nuestra función sería esta:

ID imagen del bloque con altura = 619122

Como vemos la imagen ha sido creada dinámicamente en formato PNG con el lenguaje de programación PHP, y los bytes del rawdata de la imagen están codificados en base64, mediante la función base64_encode. Y el rawdata está en la variable $im. Es decir:

data:image/png;base64,iVBORw0KGg oAAAANSUhEUgAAAEAAAABACAIAAAAlC+ aJAAAACXBIWXMAAA7EAAAOxAGVKw4bAA ABWklEQVRoge2awY2DMBRE8SoNeEvwlk ALUAKUACUkJUAJSwlQApSwtOASQgnZBm YOOU0szTsOlqOnL32bH0KsML8kr0nO9j nfzDeSM77eXP9xWECNBdRYQE1oyIOd5A +SZ5Kz86Ql+UXyieTFV8ACaiygxgJqAr vfMxK5+Q+kUfcDPmmmDefj2OGNIj5piq +ABdRYQI0F1NxShxt4feJ+f93xRn3Ebw prj0+a8Txgvj/xOVCTwVPxFbCAGguosY CaWyaDoS4PME9HgHnecP9eXvgeX1d4/6 WdYX7PeGJUfAUsoMYCaiygJgyRzGFIvJ H+vZP5Tzrwe8JPIvOliPOm9jnwmVhAjQ XUFC8QpucLPpgP8o9txn06Pb7x8hceJK 0jfk9oJ5z/zfh3i6+ABdRYQI0F1ISmwv f4a1phnsg9Pi24f7P1MeMvRI+E8+3EXz AVXwELqLGAGguo+Qen00MzJKmE8gAAAA BJRU5ErkJggg==

Saludos, me siento como bloqueado ya 😛

Minería de bitcoins explicada con lápiz y papel

Hola amigos de tardígrados. Hoy vamos a aprender a hacernos ricos en poco tiempo 🙂 En este pequeño tutorial aprenderemos cómo minar bitcoins desde cero, burlando así a las grandes granjas chinas de minería de criptomonedas.

Quizás yo no sea muy bueno en muchas cosas, pero con los años aprendí a conocerme a mi mismo bien, y descubrí que tengo ciertos talentos ocultos. Una de esas destrezas, que tenía oculta, es que soy capaz de adivinar cualquier contraseña en menos de un minuto sólo con el poder de mi mente 😛 ¿No te lo crees?. Mándame una dirección de correo electrónico tuya, y verás en tu sección de correos enviados, cómo, en poco tiempo (dependiendo del número de solicitudes de incrédulos), “me habrás enviado” un correo electrónico a albertzotkin@yahoo.com, en el que me dirás lo siguiente: “Esto prueba que sé tu contraseña y usé tu dirección de correo para enviarme esto”. Sí, amigo de Tardígrados, yo soy un superhéroe los días pares, y los impares un villano. A parte de esa destreza de adivinar mentalmente contraseñas, la cual resulta bastante sorprendente, teniendo en cuanto que soy un humano, también tengo otras cualidades ocultas, más sorprendentes aún que esa, si cabe, pero no te las voy a decir de momento, para que sigan siendo ocultas.

Hoy en día existen muchas criptomonedas, la mayoria están basadas en la tecnología del blockchain. Hasta la tostadora IoT que tengo en mi casa sería capaz de crear una criptomoneda. Sólo hay que ver que hasta Nicolás Maduro fue capaz de crear la criptomoneda Petro, con eso está dicho todo.

En este pequeño artículo que estoy escribiendo, me voy a centrar solo en el bitcoin. Hoy en día es posible comprar y vender bitcoins fácilmente, con lo que tú solito puedes llegar a enriquecerte, o a arruinarte a placer, especulando con esa moneda electrónica tan volátil. Las ventajas que tiene el bitcoin y otras monedas electrónicas, son que es un sistema descentralizado, y puede escapar fácilmente del fisco, pero a cambio, estás a expensas de fraudes, robos, y demás actividades encaminadas por terceros a dejarte sin dinero en tu billetera a cambio de nada más que disgustos. Pero, como vamos a partir de cero, es decir, de cero euros, nuestro disgusto de que nos roben cero euros sería menos del que sufriríamos si partiéramos de nuestros ahorros de toda la vida, o del dinero de la cesta de la compra.

Pero vayamos ya sin más tardar, al ajo. Para poder hacernos ricos con el bitcoin, lo primero que tenemos que hacer es conseguir una billetera (no digo monedero, porque hay ciertas personas con ciertos apellidos que me caen mal). Para ganar nuestro primer bitcoin, que a día de hoy esta a 8212.96 € en el mercado cambiario, tendremos nuestra billetera preparada para recibir moneditas calenticas recién minadas. La mejor billetera que puedes conseguir es la electrum. Una vez que hayas creado tu billetera de bitcoin electrum, guardarás tus claves offline, fuera del sistema, para que nadie que no seas tú, pueda hacerse con ellas y desplumarte. La electrum crea una clave muy peculiar, desde la que puedes acceder a tu billetera desde cualquier parte que posea conexión a internet, o con una única contraseña si la usas localmente desde tu dispositivo habitual. Dicha clave consiste en una secuencia ordenada de 12 palabras. Esa secuencia ordenada la puede memorizar, o la puedes guardar donde te plazca, pero siempre fuera del alcance de curiosos. Yo, por ejemplo, la clave de mi billetera electrum la tengo memorizada, pero también me hice un pictograma con esas 12 palabras de mi clave, porque a veces mi memoria me falla. El pictograma mnemotécnico de mi clave electrum, donde guardo algunos bitcoins, es este:

Si sientes el deseo que robarme mis criptomonedas, sólo tienes que adivinar a qué palabra corresponde cada uno de esos iconos, y voila!. Pero, si lo que deseas es enviarme algunos Satoshis, puedes hacerlo a mi clave publica:

un Satoshi es la cien millonésima parte de un bitcoin = 0.00000001 BTC. O sea que si un bitcoin se cambia actualmente por 8212.96 €, entonces 1 euro serían 12175.87 Satoshis. Lo de comprar y vender bitcoins, o con bitcoins, no tiene mayor misterio. Como habrás comprobado ya, incluso a la hora de recibir o enviar bitcoins con electrum, lo podemos hacer mediante los famosos códigos QR desde nuestros teléfonos móviles. Entonces, te estarás preguntando, cómo y cuándo vamos a empezar ya de una vez a ganar nuestros miles de Satoshis. La respuesta está en la minería de bitcoins.

La minería de bitcoins es una actividad mediante la cual van agrupando las nuevas transacciones en bloques, y estos bloques se unen a la gran cadena de bloques o blockchain. Los mineros usan potentes maquinaria de hardware a gran escala, para conseguir algún provecho, de lo contrario, esa actividad no sería rentable. Los mineros se comunican unos con otros mediante una red de nodos P2P, peer-to-peer. Usualmente lo hacen con el protocolo TCP estándar, el de los servidores web, pero no por el puerto 80 habitual, sino por los puertos 8333 o el 8332. Estos mineros de criptomonedas usan factorías llenas de cientos de procesadores fabricados y dedicados expresamente a realizar una única y sencilla operación matemática, pero han de hacerlo a gran velocidad para tener algo de probabilidad de encontrar la solución en un tiempo razonable para la rentabilidad económica. El problema con esos dispositivos es que, cada uno de ellos, es un monstruito muy ruidoso, bastante tragón de energía eléctrica, y se calienta bastante. Si juntamos en una nave industrial cientos de esos monstruitos computando a la vez sin parar las 24 horas del día, lo que obtenemos es una actividad super contaminante de ruido y calor, con energía desaprovechada por un tubo. La factura de la luz de un sólo día puede llegar a alcanzar miles de euros. La recompensa por resolver un bloque de transacciones de bitcoins es de algunas monedas, suficiente para conseguir rentabilidad.

¿En qué consiste esa sencilla operación matemática que tienen que realizar a toda velocidad esos procesadores para conseguir hacer negocio?. La solución de esa rutina operacional se llama Prueba de Trabajo. Los mineros, recolectan un conjunto de últimas transacciones del día, que están por ser confirmadas (validadas), y con ese conjunto de transacciones construyen un proyecto de bloque para ser añadido e integrado en la cadena blockchain. Junto a esas transacciones redactan la suya propia (transacción coinbase) para ganar la recompensa en el momento de dar con la solución, y todo irá incluido en el mismo proyecto de bloque. Pongamos un ejemplo concreto. Hace unos momentos, a las 17:55 de la tarde (hora de Benidorm 🙂 ), unos mineros chinos del pool AntPool han conseguido cuadrar (resolver) un nuevo bloque. Exactamente uno con el hash = 000000000000000000044b6c80648ead63c9ab7cad89f7841d6c1a420d34ba43. ¿Que qué es un hash?. Un hash es simplemente algo muy parecido a la huella de una cadena de caracteres. Existe una función hash256 que se aplica, para nuestro caso concreto, dos veces (iteración) sobre una cadena de 80 caracteres, correspondiente a la cabecera del bloque proyecto que proponen los mineros. Este bloque hallado es el número 614930 dentro del blockchain. Estos mineros chinos, en su granja con sus miles de “gallinas cibernéticas”, cacareando calientes sin parar, han puesto un huevo, por el que se están llevando al bolsillo 12.5 bitcoins, más una comisión de 0.2, es decir, un total de 12.7 bitcoins = 104304.6 euros (y eso lo hacen cada día, unas cuantas veces). La cabecera de 80 bytes, codificada en binario, de ese bloque es la siguiente:

0000000h  :  00 00 00 20 9d 88 e1 40 67 f7 f0 10 db 58 5a 2f   ;  ... ...@g....XZ/
0000010h  :  d7 28 bb c2 d8 1e e3 09 64 b7 0b 00 00 00 00 00   ;  .(......d.......
0000020h  :  00 00 00 00 82 e4 1c d2 3e c9 9f 27 d0 66 27 99   ;  ........>..'.f'.
0000030h  :  c0 cc 88 11 35 1e 33 ed d0 33 6c bd 3c b5 11 79   ;  ....5.3..3l.<..y
0000040h  :  68 a5 e4 5e 9b 67 30 5e ff 32 12 17 74 c7 f9 01   ;  h..^.g0^.2..t...

Si desglosamos la estructura de esa cabecera de 80 bytes, veremos qué parámetros la forman:

$version = 536870912 $previous_block = 0000000000000000000bb76409e31ed8c2bb28d72f5a58db10f0f76740e1889d $merkle_root = 5ee4a5687911b53cbd6c33d0ed331e351188ccc0992766d0279fc93ed21ce482 $time = 1580230555 $nbits = 387068671 $nonce = 33146740

Si ahora aplicamos la función hash256 dos veces sobre la cadena en binario de esos 80 bytes de la cabecera, obtenemos lo siguiente:

hash256(hash256(cabecera))=
000000000000000000044b6c80648ead63c9ab7cad89f7841d6c1a420d34ba43

que coincide exactamente con el hash del bloque encontrado por los mineros del Antpool. Esto significa que hemos comprobado por nosotros mismos que ese block es válido. Ya de entrada, notamos algo raro en el hash de ese bloque. Los hash256 son todos cadenas alfanuméricas (aparentemente aleatorias, porque no hay manera de saber a qué cadena de caracteres corresponde un hash determinado) de exactamente 64 caracteres, o lo que es lo mismo, de 32 bytes (independientemente del número de caracteres de la cadena sobre la que se aplica). En realidad, vemos que todo hash es un número expresado en base hexadecimal. Lo raro que notamos, es pues que existan tantos ceros seguidos a la izquierda de ese hash, de hecho es muy raro que un hash256 empiece siquiera por un único cero. En realidad, esa rareza de muchos ceros al inicio del hash es precisamente lo que se busca con tanta codicia por los mineros. Los dos parámetros clave para los mineros son el nbits y el nonce. Este ultimo es un valor que el minero está autorizado a cambiar, para ir probando hasta hallar un hash que tenga muchos ceros al inicio y que cumpla una condición. La condición la dicta el parámetro nbits. Mediante una sencilla operación el nbits se transforma en un número en base hexadecimal llamado target. Para el caso concreto del ejemplo de bloque que estamos analizando, como nbits = 387068671, el target, con esa sencilla operación, resultará ser

target=1232ff0000000000000000000000000000000000000000

Como tanto el hash del bloque como el target son números enteros (expresados en base hexadecimal, pero números), la condición, que exige Prueba de Trabajo es una simple pregunta: ¿Es el hash del bloque menor que el target?. Para contestar afirmativamente a esa pregunta los mineros empiezan a calcular el doble hash256 de la cabecera, desde nonce = 0. Y la palabra Bingo! suena bien alto en la sala cuando se halla un hash que es menor que el target.

En nuestro caso, para un nonce = 0, obtendríamos un doble hash256 de:

hash256(hash256(cabecera))=
a625bbfaf77163b53d1e30c30e8d01a7b0e00fb396b08f475d1c3eda7ecaf133

Es fácil ver que ese hash es mayor que el target. Por lo tanto, un bloque con ese nonce = 0 no sería un bloque válido. Es imposible saber qué valor de nonce cumpliría la condición. En nuestro ejemplo el nonce = 33146740 hace que se cumpla la condición, y por la tanto el bloque queda validado.Todo es puro azar, una lotería, vamos. Cuanto más juegues a la lotería más probabilidad tienes de que te toque. En eso consiste la minería de criptomonedas, con trastos ASIC, tragando hashes a velocidades endiabladas. Ludopatía pura y dura.

La velocidad de los procesadores mineros debe ser muy alta si quieren conseguir rentabilidad. Actualmente se usan en las granjas de minería de bitcoins esos chips tipo ASIC. En cada granja puede haber instalados cientos de esos ruidosos aparatos. Compremos uno de esos aparatos y pongámonos a minar bitcoins por nuestra cuenta. Podemos adquirir uno baratito por 100 euros, el AntMiner S7

Este aparatito tiene una velocidad de cálculo de 4.73 TH/s, es decir, 4.73 x 10¹² hashes por segundo, pero chupa electricidad por un tubo, ya que consume con una potencia eléctrica de 1210 vatios. Teniendo en cuenta que en España el precio del kilovatio-hora es aproximadamente de unos 0.13 euros, ese aparatito, por sí solo, durante 1 día consume 29040 kilovatios-hora, es decir, un coste por día de 3.7 euros.

¿Cuál es la probabilidad de que a la primera obtengamos un doble hash256 que cumpla esa condición de ser menor que el parámetro target?. Es como tirar un dado y ver si obtenemos un 6 a la primera tirada, pero en el caso de los hashes existirían muchos más lados que los seis de un dado normal. ¿Cuántos exactamente?. El máximo número entero de 64 cifras en representación de base hexadecimal es este:

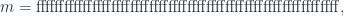
y si lo expresamos en base decimal obtendremos el número de 81 cifras

Esto significa que el número de caras de ese supuesto dado gigantesto sería de n+1. El target que se usó en el hallazgo de la solución para ese bloque era, como he dicho antes,

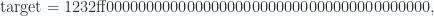
que expresado en base decimal es

Esto significa que la probabilidad de que un hash256 sea menor o igual a ese target es precisamente

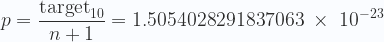
Nuestro aparatito para minar (el AntMiner S7) tiene una velocidad de v = 4.73 TH/s, por lo tanto, en un día, la probabilidad de resolver ese bloque sería de

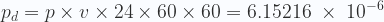
Si no me he equivocado en los cálculos, resulta ser una probabilidad demasiado baja, se necesitaría un promedio de 445 años para hallar la solución. ¿Entonces, cómo podemos ganar dinero nosotros si no nos unimos a uno de esos pool de minería?. Parece obvio que, por nuestra cuenta, las probabilidades de obtener ganancias están muy próximas a cero. De hecho los mineros en pools incluso, a veces, agotan todos los nonces, y necesitan incluir extra nonces en los proyectos de bloque para seguir probando suerte.

Y hasta aquí puedo escribir … 😛 … de momento.

¿Pero, qué diablos es realmente la gravedad? : O ¿por qué la ciencia aceptó las ideas absurdas de Einstein, que desde hace ya más de un siglo nos han llevado a un callejón sin salida, del que sólo se podrá salir definitivamente dentro de mil años o más?

Cuando Albert Einstein se vio en la cima del éxito por su Relatividad General (todos sabemos que Einstein era un genio … un genio del marketing, de la auto promoción, por supuesto), con su vanagloria en alza, y su inmenso ego, más inflado que nunca, allá por los años treinta y pico, en una de las infinitas y cuidadas entrevistas que concedía a los medios, dijo algo asi como: “Newton, perdóname; tú encontraste el único camino que, en tus tiempos, era posible para un hombre de inteligencia y capacidad creadora supremas“. O sea, en su falsa modestia, Einstein nos estaba diciendo que su capacidad creadora e inteligencia eran superiores a las de Newton. La genialidad de Einstein fue que supo vendernos humo, y lo hizo en cantidades industriales.

En cuanto al tema de la gravedad (o gravitación), a estas alturas del siglo XXI, parece ser que Einstein sólo tuvo razón en una cosa al afirmar que la gravedad no era una verdadera fuerza. El problema es que la gravedad tampoco parece ser ya ese efecto de la curvatura del espacio-tiempo, tal como tan bellamente nos lo cantaba el “poema épico” de la Relatividad General con sus matemáticas trileras, elaboradas por prestigiosos masterchefs del axioma, como Hilbert y otros, en más de un siglo de autocomplacencia. Einstein casi tuvo razón en otra cosa, pero al final se retractó, porque el precio mediático a pagar era superior al de la corrección política. Einstein, junto con Nathan Rosen, llegó a afirmar en 1936, sin tapujos, que las ondas gravitacionales no existían. Aunque ese concepto de las ondas gravitationales lo había deducido él mismo de su misma Relatividad General, unos cuanto años antes, al final dio su brazo a torcer, desistió de su “descabellada idea”, porque la presión mediática era inmensa, y su prestigio, su reputación social y académica estaban en juego.

En este pequeño artículo que hoy os presento, veremos qué es realmente la gravedad, y por qué las ondas gravitacinales no pueden existir si la gravedad es lo que aquí voy a afirmar que es.

La gravedad es una fuerza entrópica. Si, ya sé que desde la física oficial, tratan de barrer toda hipótesis que afirme que la gravedad es una fuerza entrópica. Sobre todo, existen infinitos artículos (mainstreamófilcos = muy del consenso oficial) que aparentemente demuestran que la Gravedad Entrópica de Verlinde es inconsistente. El dogma oficial, cuando quiere sofocar algo que incomoda a la doctrina reinante, siempre se basa en demostrar aparentemente que ese algo es inconsistente. El problema es que al final todo se reduce a creer o no que la demostración de la inconsistencia es consistente. La gravedad entrópica de Verlinde, no es toda la verdad sobre la afirmación de que la gravedad es una fuerza entrópica. Los que intentan desacreditar a Verlinde por su teoría entrópica de la gravedad, siempre basan su armas en que dicha teoría posee errores que la reducen a una mera expresión de la teoría clásica de Newton, no ya siquiera a una MOND, y por lo tanto, como la teoría clásica de Newton es incorrecta según el consenso de los mainstreamófilos, porque la correcta es la de Einstein, asi de incorrecta debe ser la de Verlinde . Pero, examinando a fondo esta teoría de la Gravedad Entrópica de Verlinde, se llega a la conclusión de que basicamente es correcta, y en lo único que falla es en la elección de los modelos matemáticos y termodinámicos para deducirla desde primeros principios. En esencia, de lo que carece la Gravedad Entrópica de Verlinde es de la componente gravitomagnética, la cual hay que deducir también desde principios termodinámicos. Eso fue lo que yo hice hace tiempo en mi artículo: Gravedad Cuántica: Análisis pormenorizado de la componente entrópica de la gravedad. Pero veamos sucintamente en que consiste la Gravedad Entrópica de Verlinde, y por qué la atacaban tan furibondamente desde el consenso de los mainstreamófilos.

A estas alturas del siglo XXI, aún se pueden leer blogs de ciencia, donde supuestos científicos (y científicas) hacen afirmaciones sobre agujeros negros (hipotéticos objetos, de cuya existencia no tendremos nunca una prueba definitiva) tales como: “Dos agujeros negros uniéndose no emiten radiación electromagnética, porque los agujeros negros no están hechos de materia que pueda emitir esa clase de radiación. Pueden estar rodeados de materia que sí la emite, pero es demasiado pequeña para ser observada.” Es decir, siguen tratando el espacio-tiempo como si fuera una sustancia, una especie de éter flexible que pueda ser estirado, retorcido o curvado. Que yo sepa, el espacio-tiempo no existe físicamente hasta que no se demuestre experimentalmente por separado que el espacio existe y que el tiempo existe. Pero mucho me temo que ambas entidades que tanto se emplean en física, son más axiomas o postulados que algo real existente en la naturaleza.

Hace ya algún tiempo un tal Erik Verlinde publicó un artículo en el que supuestamente deducía la ley de gravitación universal de Newton desde primeros principios, incluso dedujo las ecuaciones de campo de Einstein de la Relatividad General, concluyendo que la gravedad es una fuerza entrópica, es decir una fuerza que no es fundamental y que emerge naturalmente del aumento de entropía de los sistemas materiales. Verlinde usó el principio holográfico y las conocidas leyes de la termodinámica, junto con algunas cosillas más, para deducir dicha fuerza entrópica. Las fuerzas entrópicas emergen desde el microcosmos hacia el macrocosmos debido a que los sistemas materiales tienden a adoptar estados de máxima entropia. Cuando estiras una goma elástica debes de ejercer una fuerza para contrarrestar temporalmente su estado maximizado de entropía. Al estirar la goma estás rebajando su entropia, y por lo tanto la goma se opone a ese cambio ejerciendo una fuerza en sentido contrario que intenta restaurar su estado de máxima entropía.

Pero, como vamos a ver ahora, esa fuerza entrópica deducida por Verlinde desde primeros principios, y que emerge siendo la fuerza de gravitación de Newton, es sólo una componente de la gravedad total. En concreto vamos a ver cómo esa componente entrópica es engullida brutalmente por un tiburón cuántico que habita en las profundidades del microcosmos termodinámico.

Comencemos expresando la Primera Ley de la Termodinámica para sistemas homogeneos cerrados:

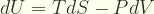(1)

donde dU es el cambio de energía interna, T es la temperatura, dV es el cambio de volumen, dS es el cambio de entropia, y P es la presión. Sabemos que PdV es el cambio de energía libre del sistema, por lo tanto puede ser expresada como suma de los cambios de energía de cada uno de los microestados

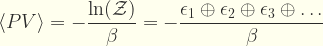(2)

Donde e_s representa la energía del microestado s, Z es la función de partición, y β es menos el inverso del producto de la temperatura por la constante de Boltzmann:

La ecuación (1) para un proceso con presión y temperatura constantes queda así:

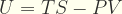(3)

por lo tanto sustituyendo (2) en (3) tenemos:

(4)

Según el postulado fundamental de la mecánica estadística, la entropía S es directamente proporcional al logaritmo del número Ω de microestados:

es decir

(5)

por lo que (4) lo podemos calcular más fácilmente:

(6)

Esta energía interna U es lo que en gravedad debe identificarse como la energía potencial gravitatoria, la cual si es dividida por la masa m de una partícula de prueba tendremos el potencial gravitatorio (con todas sus componentes) en el punto espacial donde está localizada dicha partícula:

(7)

Recapitulemos. La componente entrópica debe ser identificada con la gravitación clásica de Newton, y la componente de energía libre (PV) debe ser identificada con lo que se llama gravitomagnetismo. O lo que es lo mismo, la función de partición Z mapea dicho gravitomagnetismo, mientras que el número Ω de microestados mapea la componente estática de gravitación Newtoniana.

Pongamos un pequeño ejemplo. Supongamos que queremos calcular el número Ω de microestados de un sistema gravitatorio binario, con masas M y m. Igualamos el potencial gravitatorio así:

pero en β está incluida la temperatura T, por lo tanto si igualamos esa temperatura con la temperatura de Unhru: ,

y la aceleración a la igualamos a la aceleración del campo gravitatorio estático, a = g:

Por lo que el número Ω de microestados para ese sistema gravitatorio será:

Las fuerzas entrópicas están muy relacionadas con los paseos aleatorios

y por lo tanto, la gravedad es una interacción estrechamente relacionada con lo que se llama paseos aleatorios de máxima entropía.

Supremacía cuéntica

No, no me he equivocado en el título. He escrito cuéntica en lugar de cuántica a propósito, para resaltar que la supuesta supremacía cuántica es un cuento chino que nos están contando. Vamos, que “naranjas de la China“.

Cuando una computadora cuántica haga cosas que una computadora clásica no pueda hacer en tiempo y recursos razonables, entonces diremos que esa computadora ha alcanzado supremacia cuantica.

La revista Nature nos cuenta estos días que Google ha alcanzado oficialmente la supremacía cuántica. Hace poco, LIGO nos contó también que habían alcanzado la supremacía gravitacional, y lo anunciaron al mundo, como el gran hito científico del siglo XXI, y les concedieron hasta un Premio Nobel de Física, tú. “Naranjas de la China“, cuentos chinos. La única supremacía real que existe es la fanfarronería científica yanqui. Estamos asistiendo al triunfo de sofisticadas técnicas mediáticas para propagar ideas (supuestamente científicas), técnicas que Goebbels ya empleó con éxito para la propaganda Nazi.

Con la computación cuántica pasa lo mismo que con la fusión nuclear: son eternas promesas de hitos científico-técnicos que nunca llegan a ser una realidad. Los expertos ponen como excusa que es muy difícil evitar la decoherencia cuántica, para el primer caso, y conseguir un adecuado confinamiento de plasma, para el segundo. Pero, habría que empezar a pensar ya que el motivo por el que realmente no se han conseguido aún esos hitos científico-técnicos está más en la teoría científica, es decir, en los modelos teóricos, que en llevarlos a la práctica. Es muy probable que los modelos teóricos que predicen tanto la computación cuántica como la fusión termonuclear no sean correctos, o les falte algo insospechado. En cualquier caso, no parece razonable asistir a estos espectáculos de supuesta supremacía en no sé qué materias, como si fuera una competición olímpica donde todos los atletas estuvieran dopados.

Pero, ¿qué cuento chino nos está contando Google respecto a su supuesta supremacía cuántica conseguida, que dicen que ya es oficial y todo?: En el resumen del documento presentado nos dicen:

La esperanza en los computadores cuánticos es que ciertas tareas computacionales podrían ser realizadas exponencialmente más rápido con un procesador cuántico que con un procesador clásico. El reto fundamental consiste en construir un procesador de alta fidelidad capaz de ejecutar algoritmos cuánticos en un espacio computacional exponencialmente grande. En este documento presentamos un informe sobre el uso de un procesador cuántico con cubits programables de supercomputación para crear estados cuánticos en 53 cubits, representando un espacio computacional de dimensión 2⁵³ (aproximadamente 10¹⁶). Medidas de experimentos repetidos muchas veces proporcionan una muestra de la resultante distribución de probabilidad, la cual verificamos usando simulaciones clásicas. Nuestro procesador cuántico Sycamore tarda unos 200 segundos en muestrear una instancia de circuito cuántico, mientras que el mejor computador clásico actual tardaría en realizar esa misma tarea unos 10 mil años. Esta dramática mejora de la velocidad comprada con la de cualquier algoritmo clásico actual conocido resulta ser una realización experimental de supremacía cuántica, para esta tarea computacional específica, y presagia un cambio de paradigma en el campo de la computación.

O sea, que los chicos de Google han construido un procesador cuántico de 53 cubits (en principio eran 54, pero uno se estropeó), llamado Sycamore, y lo han programado para que ejecute un tarea específica, sabiendo de antemano que esa misma tarea, ejecutada en un procesador clásico, tardaría 10 mil años en ser completada.

Fig. 1: Procesador Sycamore.

a, Diseño del procesador, mostrando una matriz rectangular de 54 cubits (gris), cada uno conectado a sus cubits anejos mediando acopladores (azul). El cubit no operativo (estropeado), situado en la parte superior del esquema, está sólo perfilado (no relleno en color gris). b, fotografía del chip Sycamore.

Pero, ¿cómo construyen esos cubits?. Para provechar ciertas propiedades de los estados cuánticos, llamadas superposición y entrelazamiento, entre otras propiedades y efectos también bastante raritos, que describe la Mecánica Cuántica, usan átomos, y hay que conseguir, mediante temperaturas muy próximas al cero absoluto (-273,144 °C), que los electrones de esos átomos giren en un sentido y hacia el contrario al mismo tiempo. Ese sería el efecto de superposición cuántica. Es decir, no seria que unos electrones, dentro del mismo átomo, giraran en un sentido y otros en el contrario, sino que cada electrón girase en un sentido y el contrario a la vez. Algo impensable y absurdo para un cuerpo macroscópico, pero no tanto para las partículas subatómicas, que se rigen por reglas de la mecánica cuántica. El problema de la superposición está en que cuando se intenta medir el estado cuántico, aparece la decoherencia, el cubit de pronto se transforma en un simple bit clásico. Ese es el famoso quebradero de cabeza llamado problema de la medida

¿De verdad ha conseguido Google la supremacía cuántica?. Uno de los mayores expertos en computación cuántica es el murciano Dario Gil. Este murciano, director mundial de IBM Research, nada menos, opina que el procesador cuántico Sycamore de Google “es una pieza especializada de hardware diseñada para resolver un solo problema y no un ordenador cuántico de propósito general, a diferencia de los desarrollados por IBM”. Es decir, aunque podría ser cierto que habrían completado una tarea de muestreo en 200 segundos, mientras que el superordenador Summit de IBM habría tardado 10 mil años en completar esa misma tarea, el Sycamore sólo serviría para realizar esa tarea y ninguna otra más. Es como construir un ordenador que sólo supiera sumar 2+2, y nada más. Si Dario Gil tiene razón, que yo creo que la tiene, para resolver problemas reales mediante computación cuántica habría, no sólo que programar los algoritmos (software) cuánticos, sino construir físicamente el hardware especifico para ese problema en concreto. O sea, cada problema requeriría de un hardware especifico, y sólo valdría para ese problema. Por ejemplo, supongamos que queremos factorizar el número entero semiprimo RSA1024, que posee 1024 cifras binarias (309 cifras decimales). ¿Valdria la pena construir un procesador cuántico especifico para hallar, en un tiempo razonablemente corto, los dos números primos que multiplicados dan ese número RSA1024?. Si el premio es superior al coste, si valdría la pena 🙂 , pero hay que tener en cuenta que una vez factorizado ese número SRA concreto, nuestro costoso chip cuántico no valdría para nada más, y habría que tirarlo a la basura o aprovechar sus piezas para construir otro chip distinto para resolver otro problema distinto. Nuestro amigo murciano, Dario Gil, es un genio, y sabe muy bien de qué habla.

Pero, en mi opinión, lo que Google nos ha traído de momento, en lugar de supremacía cuántica, son naranjas de la China.

Saludos cordiales, y para nada supremacistas 😉

Hola KATRIN, ¿sabes que los neutrinos viajan más rápido que la luz, y cuánto ridículo hace la ciencia actual negándolo?

Estos días se habla mucho en los foros científicos del experimento KATRIN, que ha publicado resultados estimando un valor máximo para la masa de los neutrinos. En este experimento científico se examina el espectro de la desintegración beta (emisión de electrones) del Tritio, mediante un potente y peculiar espectómetro

Transporte por las calles de Karlsruhe (Alemania) de parte del espectrómetro del experimento KATRIN

En esta desintegración beta del Tritio, además de electrones, se emiten trillones de anti-neutrinos electrónicos por segundo. La idea central del experimento KATRIN es muy simple: Si el neutrino tiene masa, entonces siempre debe corresponder a la cantidad equivalente de energía, según la ecuación E = m c², y el espectro del electrón debería reflejar un deficit en su energía total exactamente igual a esa cantidad, y mostrar una forma diferente en dicho espectro.

En el artículo científico que describe los resultados de las mediciones, titulado, “An improved upper limit on the neutrino mass from a direct kinematic method by KATRIN“, y cuyo preprint puede encontarse en arXiv, aqui, y donde firman más de 210 autores de más de 36 institutos, centros de investigación y universidades, se comete una de las tropelías más flagrantes y ridículas de la historia de la ciencia. Se trata del conocido sesgo cognitivo, pero esta vez se deja al descubierto con tal evidencia y desdén que más parece que lo hagan a propósito que un descuido. Veamos paso a paso en qué consiste ese sesgo y por qué los tontos del culo de los blogs que le siguen el juego a lo políticamente correcto del consenso oficial, hacen todo lo posible por obviar esa tropelía, mirando para otro lado y silbando, cuando no mintiendo.

En el apartado de resultados finales de dicho artículo, se dice que la mejor estimación para el cuadrado de la masa del neutrino es de

es decir, para cualquiera que sepa leer estos resultados tenemos un valor medio que es un número real negativo de -1.0 electrovoltios al cuadrado, afectado con cierta incertidumbre de medida. Es decir, tenemos que el cuadrado de un número es un valor negativo. Eso solo es posible si la masa de un neutrino es un número imaginario puro. O sea un valor medio, expresado por el número complejo:

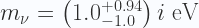
Por su puesto, el valor central de -1.0 está a simplemente una desviación típica de cero. La pregunta es ¿por qué la región negativa de la masa al cuadrado está excluida, y considerada como no física, es decir, como algo que no puede darse físicamente?. Por lo tanto, el sesgo cognitivo está en que, a priori, se está diciendo que el valor negativo del cuadrado de una masa es algo físicamente imposible, cuando de hecho debería ser una cuestión a dilucidar experimentalmente, nunca a priori. ¿Cuantas tropelías más nos están metiendo dobladas?. Esta que apunto hoy aquí es descaradamente evidente.

Esta tropelía cometida en el artículo científico del experimento KATRIN, que ya he apuntado arriba, fue debidamente denunciada por Alan Chodos, el cual elevó un comentario suyo a arXiv, dejando en evidencia esa chapuza de artículo firmada por más de 210 autores de más de 36 institutos, centros de investigación y universidades.

Comentario de: Alan Chodos

Departamento de Física, Universidad de Texas, Arlington

alan.chodos@uta.edu

Sumario: Hacemos notar que el valor central del experimento KATRIN tiene masa al cuadrado negativa, y nos preguntamos por qué se excluye del análisis estadístico a priori.

Introducción, discusión y conclusiones: El nuevo límite superior para la masa del neutrino electrónico, que ha sido publicado recientemente del experimento KATRIN, no sólo merece ser destacado por su gran precisión de medida, sino también por el hecho de que el valor central de dicha medida resulta ser un valor negativo, representando una masa al cuadrado, lo cual viene siendo ya habitual en una larga tradición de medidas de las masas de los neutrinos, desde hace ya varias décadas.

Por su puesto, el valor central resulta estar a una desviación típica respecto a cero. Por lo tanto, resulta absolutamente adecuado decir que se trata de un límite superior, y no una medida de una masa no nula. Sin embargo, tal y como se indica en el informe, la región negativa de la masa al cuadrado está excluida a priori, y marginada (ignorada) como algo no físico (algo que no puede darse en la naturaleza) al realizar los análisis estadísticos, siguiendo la practica de muchos de los autores que firman el artículo.

El propósito de esta breve reseña es señalar que esa es una mala praxis, una restricción inapropiada. Que los neutrinos tengan o no una masa al cuadrado negativa, es una cuestión experimental. Al menos, los autores deberían incluir un análisis alternativo en el que la posibilidad de una masa al cuadrado negativa fuera permitida.

Los trabajos teóricos sobre neutrinos en espacio-tiempo superlumínico se remontan hasta la mitad de los años ochenta. Muchas ideas especulativas al respecto puede que no sean muy relevantes, pero a pesar de todo, la posibilidad de que el neutrino sea un taquión sigue abierta, y no debería ser descartada, y menos aún, descartada antes de iniciar cualquier análisis.

En conclusión: si los neutrinos poseen masa imaginaria cuando aplicamos los formalismos de la Relatividad Especial de Einstein, eso quiere decir que son taquiones (partículas que viajan a velocidades superiores a la de la luz). Con lo cual, tanto el Modelo Estándar de la Física Cuántica, como la Teoría de la Relatividad de Einstein, se pueden ir ya, sin demora, por el sumidero de la historia de la ciencia, a pesar de lo que nos diga la famosa ciencióloga (drag queen, y reina del chismorreo mainstreamófilo) la Mula Francis.

Saludos