Hola KATRIN, ¿sabes que los neutrinos viajan más rápido que la luz, y cuánto ridículo hace la ciencia actual negándolo?

Estos días se habla mucho en los foros científicos del experimento KATRIN, que ha publicado resultados estimando un valor máximo para la masa de los neutrinos. En este experimento científico se examina el espectro de la desintegración beta (emisión de electrones) del Tritio, mediante un potente y peculiar espectómetro

Transporte por las calles de Karlsruhe (Alemania) de parte del espectrómetro del experimento KATRIN

En esta desintegración beta del Tritio, además de electrones, se emiten trillones de anti-neutrinos electrónicos por segundo. La idea central del experimento KATRIN es muy simple: Si el neutrino tiene masa, entonces siempre debe corresponder a la cantidad equivalente de energía, según la ecuación E = m c², y el espectro del electrón debería reflejar un deficit en su energía total exactamente igual a esa cantidad, y mostrar una forma diferente en dicho espectro.

En el artículo científico que describe los resultados de las mediciones, titulado, “An improved upper limit on the neutrino mass from a direct kinematic method by KATRIN“, y cuyo preprint puede encontarse en arXiv, aqui, y donde firman más de 210 autores de más de 36 institutos, centros de investigación y universidades, se comete una de las tropelías más flagrantes y ridículas de la historia de la ciencia. Se trata del conocido sesgo cognitivo, pero esta vez se deja al descubierto con tal evidencia y desdén que más parece que lo hagan a propósito que un descuido. Veamos paso a paso en qué consiste ese sesgo y por qué los tontos del culo de los blogs que le siguen el juego a lo políticamente correcto del consenso oficial, hacen todo lo posible por obviar esa tropelía, mirando para otro lado y silbando, cuando no mintiendo.

En el apartado de resultados finales de dicho artículo, se dice que la mejor estimación para el cuadrado de la masa del neutrino es de

es decir, para cualquiera que sepa leer estos resultados tenemos un valor medio que es un número real negativo de -1.0 electrovoltios al cuadrado, afectado con cierta incertidumbre de medida. Es decir, tenemos que el cuadrado de un número es un valor negativo. Eso solo es posible si la masa de un neutrino es un número imaginario puro. O sea un valor medio, expresado por el número complejo:

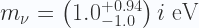
Por su puesto, el valor central de -1.0 está a simplemente una desviación típica de cero. La pregunta es ¿por qué la región negativa de la masa al cuadrado está excluida, y considerada como no física, es decir, como algo que no puede darse físicamente?. Por lo tanto, el sesgo cognitivo está en que, a priori, se está diciendo que el valor negativo del cuadrado de una masa es algo físicamente imposible, cuando de hecho debería ser una cuestión a dilucidar experimentalmente, nunca a priori. ¿Cuantas tropelías más nos están metiendo dobladas?. Esta que apunto hoy aquí es descaradamente evidente.

Esta tropelía cometida en el artículo científico del experimento KATRIN, que ya he apuntado arriba, fue debidamente denunciada por Alan Chodos, el cual elevó un comentario suyo a arXiv, dejando en evidencia esa chapuza de artículo firmada por más de 210 autores de más de 36 institutos, centros de investigación y universidades.

Comentario de: Alan Chodos

Departamento de Física, Universidad de Texas, Arlington

alan.chodos@uta.edu

Sumario: Hacemos notar que el valor central del experimento KATRIN tiene masa al cuadrado negativa, y nos preguntamos por qué se excluye del análisis estadístico a priori.

Introducción, discusión y conclusiones: El nuevo límite superior para la masa del neutrino electrónico, que ha sido publicado recientemente del experimento KATRIN, no sólo merece ser destacado por su gran precisión de medida, sino también por el hecho de que el valor central de dicha medida resulta ser un valor negativo, representando una masa al cuadrado, lo cual viene siendo ya habitual en una larga tradición de medidas de las masas de los neutrinos, desde hace ya varias décadas.

Por su puesto, el valor central resulta estar a una desviación típica respecto a cero. Por lo tanto, resulta absolutamente adecuado decir que se trata de un límite superior, y no una medida de una masa no nula. Sin embargo, tal y como se indica en el informe, la región negativa de la masa al cuadrado está excluida a priori, y marginada (ignorada) como algo no físico (algo que no puede darse en la naturaleza) al realizar los análisis estadísticos, siguiendo la practica de muchos de los autores que firman el artículo.

El propósito de esta breve reseña es señalar que esa es una mala praxis, una restricción inapropiada. Que los neutrinos tengan o no una masa al cuadrado negativa, es una cuestión experimental. Al menos, los autores deberían incluir un análisis alternativo en el que la posibilidad de una masa al cuadrado negativa fuera permitida.

Los trabajos teóricos sobre neutrinos en espacio-tiempo superlumínico se remontan hasta la mitad de los años ochenta. Muchas ideas especulativas al respecto puede que no sean muy relevantes, pero a pesar de todo, la posibilidad de que el neutrino sea un taquión sigue abierta, y no debería ser descartada, y menos aún, descartada antes de iniciar cualquier análisis.

En conclusión: si los neutrinos poseen masa imaginaria cuando aplicamos los formalismos de la Relatividad Especial de Einstein, eso quiere decir que son taquiones (partículas que viajan a velocidades superiores a la de la luz). Con lo cual, tanto el Modelo Estándar de la Física Cuántica, como la Teoría de la Relatividad de Einstein, se pueden ir ya, sin demora, por el sumidero de la historia de la ciencia, a pesar de lo que nos diga la famosa ciencióloga (drag queen, y reina del chismorreo mainstreamófilo) la Mula Francis.

Saludos

Neutrinos superlumínicos: desintegración de un pión

Hola amigos de Tardígrados. Hoy vamos a ver cómo se desintegra un pión (pi mesón). En concreto veremos el modo principal en que decae un pión con carga eléctrica positiva. Los pi mesones con carga tienen una masa de 139.6 MeV/c², y una vida media de 2.6 × 10?8 s. Se desintegran debido a la interacción débil. El modo de desintegración más común es una desintegración leptónica hacia un muón y un muón neutrino, la cual ocurre el 99% de las veces:

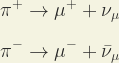(1)

Un pión π⁺ está constituido por un par de quarks, en concreto, un quark up y un quark anti-down, y el modo de desintegración principal es como muestra el siguiente diagrama:

Este pi mesón decae en reposo, por lo tanto, las leyes de conservación serán estas:

Pero, en el capítulo anterior vimos cómo los neutrinos no pueden estar en reposo auque sean producto de la desintegración de partículas que estaban en reposo. Para este cálculo teórico usaré la relación de dispersión neutrínica descubierta por mi en el capítulo anterior: Así, tendremos:

Observamos también que si el momento del neutrino no es cero, entonces tampoco debe ser cero el momento del muón. En concreto, ese momento debe ser exactamente opuesto e igual en magnitud al del neutrino. Escalarmente serían:

Si suponemos que el muón se mueve con una velocidad sublumínica, por ejemplo, con una β = 1/20, obtendremos una β para el neutrino muónico de:

Es decir, ese neutrino muónico superaría en 4 veces la velocidad de la luz en el vacío. Para un rango de velocidades muónicas que van desde β = 0 hasta β = 1, tendríamos la siguiente gráfica del intervalo de velocidades para el neutrino:

Saludos

¿Por qué el cuadrado de la masa de un neutrino es un valor negativo?

Desde hace muchos años se sabe que el cuadrado de las masas (medidas) de los neutrinos es siempre un valor negativos, lo que resulta extraño, ya que matemáticamente tendríamos una masa imaginaria. Para reconciliar este aparente sinsentido con la razón, se propuso ya desde hace tiempo que los neutrinos debían ser fermiones que se mueven a velocidades superluminicas.

El cuadrado de la masa de un neutrino se midió sistemáticamente en experimentos donde tenia lugar la desintegración del Tritio, que produce emisiones beta de baja energía. Esas mediciones de la masa de los neutrinos se realizaba ajustando la forma del espectro de emisión las partículas beta cerca de sus puntos extremos. En muchos de esos experimentos se encontró que los cuadrados de esas masas daban significativos e inequívocos valores negativos. La mayoría de esos datos están registrados en ”Review of Particle Physics, 2000” (Review of Particles Physics, Euro. Phys. Jour. C15, 350-353 (2000).). Dos de esos experimentos en 1999 dieron en sus medias ponderadas el siguiente valor:

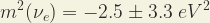(1)

Sin embargo, otras nueve medidas de experimentos realizados entre 1991-1995 no se usan como medias. Por ejemplo, el valor de:

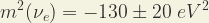(2)

con un 95% de nivel de confianza se midió en el LLNL en 1995. El valor negativo del cuadrado de las masas de los neutrinos significa que la relación de dispersión de la energía total y el momento es simplemente:

(3)

Desde la teoría de la Relatividad Especial todo esto conduce a pensar que las velocidades de esos neutrinos es superior a c. Por ejemplo, la energía total es desde el punto de vista de esa teoría:

(4)

implicaría que esa energía es un número complejo puro. Y lo mismo ocurriría con su momento lineal:

(5)

y eso implicar, a su vez, que ha de ser:

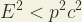
(6)

Todo este sinsentido ocurre cuando usamos los formalismos de la Relatividad Especial para describir la energía y el momento lineal de los neutrinos. Veamos ahora, qué ocurre cuando usamos los formalismos de la Relatividad Galileana Completa:

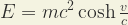(7)

(8)

Observamos, con agrado, que con estos formalismos matemáticos de la Relatividad Galileana Completa, no obtenemos absurdos como energías y momentos que sean magnitudes imaginarias, sino que son números reales, y con la única condición de que la inecuación (6) se cumple para los neutrinos. Por lo tanto los neutrinos podrían ser taquiones, una clase de partículas, que viajarían a velocidades superluminicas. La relación de dispersión entre energía y momento para los fermiones (tardiones) y para los taquiones, se puede representar gráficamente de forma paramétrica así:

Vemos que son hipérbolas, donde, obviamente, el parámetro es la β = v/c, y las lineas discontinuas, son las asíntotas, que representa la velocidad de la luz, c (es decir para β = 1) . La ecuación de una hipérbola es:

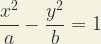(9)

y en forma paramétrica con coseno y seno hiperbólicos es:

(10)

Esto significa que, para los fermiones, la relación de dispersión entre energía y momento es:

(11)

Para partículas que sean taquiones, como supuestamente son los neutrinos, la relación de dispersión entre su energía y momento obedece a una transformación de inversión como la siguiente:

(12)

Es decir, la gráfica es una hipérbola orientaba norte-sur, como la representada en la figura anterior. Por lo tanto, para los neutrinos tenemos la relación:

(13)

La conclusión de todo esto es clara: si aplicamos a los neutrinos las mismas leyes y relaciones entre energía y momento que aplicamos a los fermiones, obtenemos masas imaginarias o velocidades superluminicas. Es decir, los formalismos fermiónicos aplicados a neutrinos nos ofrecen valores negativos para los cuadrados de sus masas. Pero si aplicamos una relación de dispersión energía-momento distinta, no obtenemos esos valores imaginarios sino valores reales. Los neutrinos, no tienen por que viajar a velocidades superluminicas, simplemente obedecen la relación E²- p²c² = – m²c4. Por el contrario, los leptones, que tampoco tienen por que viajar a velocidades superlumínicas, poseen esta otra relación de dispersión: E²- p²c² = m²c4.

Analicemos brevemente una desintegracion de Michel para un muón:

En dicha desintegración, el muón decae hacia un electrón, más un antineutrino electrónico y un muón neutrino. Si desglosamos la dispersión leptónica, obtenemos:

esas relaciones ya no nos ofrecen ni velocidades superlumínicas, ni masas imaginarias, ni valores negativos de cuadrados de masas, porque las relaciones de dispersión para los neutrinos que usamos aquí son distintas a las que propone la Relatividad Especial. Si suponemos que esa desintegración del muón se realizó en reposo, entonces las leyes de conservación son:

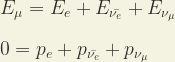(14)

Donde E_μ = m_μc², y p_μ = 0, porque el muón se supone en reposo.

Si observamos detenidamente la relación de dispersión entre energía y momento para los neutrinos aquí propuesta, nos daremos cuenta de que si suponemos que un neutrino está en reposo entonces su momento lineal no sería cero, sino:

(15)

Esto implica ni más ni menos que un neutrino en reposo es simplemente una partícula que viaja a la velocidad de la luz, c. ¿Contradicción?. ¿Cómo es posible que una partícula esté moviéndose a una velocidad c si hemos dicho que está en reposo?. En realidad, le pasa lo mismo que a los fotones, lo que ocurre es que los neutrinos sí poseen masa y aún así se mueven a velocidad c. Este fenómeno no puede ser descrito con los formalismos de la Relatividad Especial.

Saludos