TARDÍGRADOS

Ciencia en español -ʟᴀ ʀᴀᴢóɴ ᴇsᴛá ᴀʜí ғᴜᴇʀᴀ-

«
»

¿Por qué el cuadrado de la masa de un neutrino es un valor negativo?

Posted by Albert Zotkin on June 10, 2016

Desde hace muchos años se sabe que el cuadrado de las masas (medidas) de los neutrinos es siempre un valor negativos, lo que resulta extraño, ya que matemáticamente tendríamos una masa imaginaria. Para reconciliar este aparente sinsentido con la razón, se propuso ya desde hace tiempo que los neutrinos debían ser fermiones que se mueven a velocidades superluminicas.

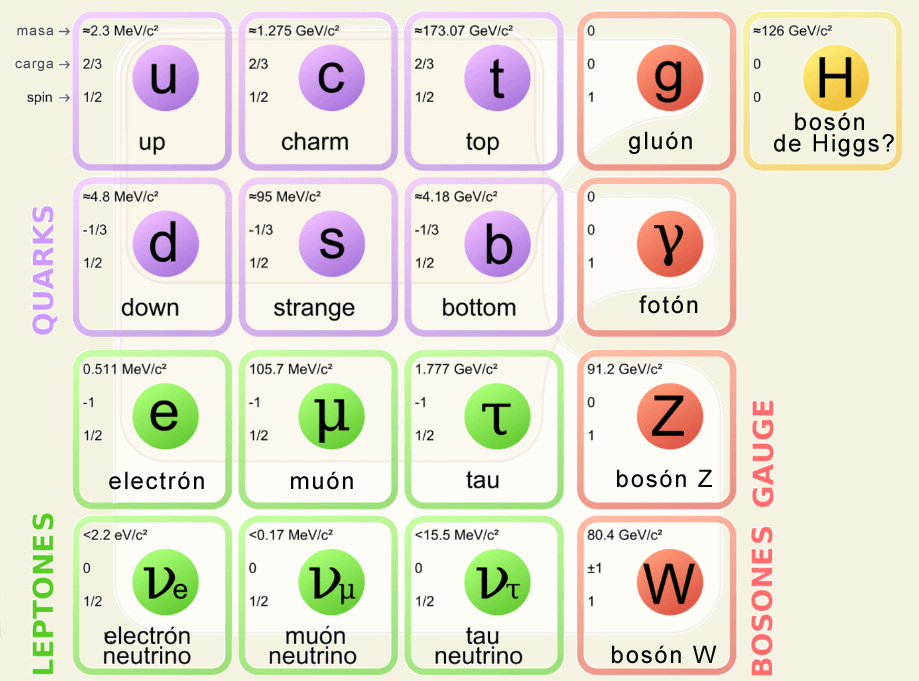
lepto-quarks

El cuadrado de la masa de un neutrino se midió sistemáticamente en experimentos donde tenia lugar la desintegración del Tritio, que produce emisiones beta de baja energía. Esas mediciones de la masa de los neutrinos se realizaba ajustando la forma del espectro de emisión las partículas beta cerca de sus puntos extremos. En muchos de esos experimentos se encontró que los cuadrados de esas masas daban significativos e inequívocos valores negativos. La mayoría de esos datos están registrados en ”Review of Particle Physics, 2000” (Review of Particles Physics, Euro. Phys. Jour. C15, 350-353 (2000).). Dos de esos experimentos en 1999 dieron en sus medias ponderadas el siguiente valor:

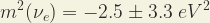\displaystyle m^2(\nu_e) = -2.5 \pm 3.3 \; eV^2 (1)
Sin embargo, otras nueve medidas de experimentos realizados entre 1991-1995 no se usan como medias. Por ejemplo, el valor de:

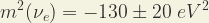\displaystyle m^2(\nu_e) = -130 \pm 20 \; eV^2 (2)
con un 95% de nivel de confianza se midió en el LLNL en 1995. El valor negativo del cuadrado de las masas de los neutrinos significa que la relación de dispersión de la energía total y el momento es simplemente:

\displaystyle E^2 - p^2 c^2 = m^2(\nu_e)c^4 \; \textless\; 0 (3)
Desde la teoría de la Relatividad Especial todo esto conduce a pensar que las velocidades de esos neutrinos es superior a c. Por ejemplo, la energía total es desde el punto de vista de esa teoría:

\displaystyle E = mc^2 \gamma = \cfrac{mc^2}{\sqrt{1-\tfrac{v^2}{c^2}}} (4)
implicaría que esa energía es un número complejo puro. Y lo mismo ocurriría con su momento lineal:

\displaystyle p = \cfrac{mv}{\sqrt{1-\tfrac{v^2}{c^2}}} (5)
y eso implicar, a su vez, que ha de ser:

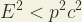
\displaystyle E^2 \;\textless\; p^2 c^2

(6)
Todo este sinsentido ocurre cuando usamos los formalismos de la Relatividad Especial para describir la energía y el momento lineal de los neutrinos. Veamos ahora, qué ocurre cuando usamos los formalismos de la Relatividad Galileana Completa:

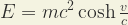\displaystyle E = mc^2 \cosh \tfrac{v}{c} (7)
\displaystyle p = mc \sinh \tfrac{v}{c} (8)
Observamos, con agrado, que con estos formalismos matemáticos de la Relatividad Galileana Completa, no obtenemos absurdos como energías y momentos que sean magnitudes imaginarias, sino que son números reales, y con la única condición de que la inecuación (6) se cumple para los neutrinos. Por lo tanto los neutrinos podrían ser taquiones, una clase de partículas, que viajarían a velocidades superluminicas. La relación de dispersión entre energía y momento para los fermiones (tardiones) y para los taquiones, se puede representar gráficamente de forma paramétrica así:

e-p

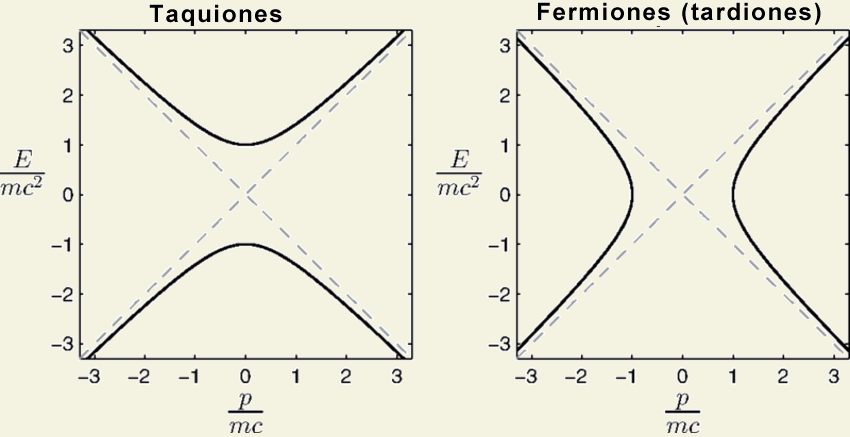
Vemos que son hipérbolas, donde, obviamente, el parámetro es la β = v/c, y las lineas discontinuas, son las asíntotas, que representa la velocidad de la luz, c (es decir para β = 1) . La ecuación de una hipérbola es:

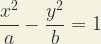\displaystyle \frac{x^2}{a}-\frac{y^2}{b}=1 (9)
y en forma paramétrica con coseno y seno hiperbólicos es:

\displaystyle \cosh^2 u -\sinh^2 u =1 (10)
Esto significa que, para los fermiones, la relación de dispersión entre energía y momento es:

\displaystyle \cosh^2 \left(\frac{v}{c}\right) -\sinh^2 \left(\frac{v}{c}\right) =1 \\ \\ \\ \cfrac{E}{mc^2}= \cosh \left(\frac{v}{c}\right) \\ \\ \\ \cfrac{p}{mc}= \sinh \left(\frac{v}{c}\right) (11)
Para partículas que sean taquiones, como supuestamente son los neutrinos, la relación de dispersión entre su energía y momento obedece a una transformación de inversión como la siguiente:

\displaystyle \cfrac{E}{mc^2}= \sinh \left(\frac{v}{c}\right) \\ \\ \\ \cfrac{p}{mc}= \cosh \left(\frac{v}{c}\right) (12)
Es decir, la gráfica es una hipérbola orientaba norte-sur, como la representada en la figura anterior. Por lo tanto, para los neutrinos tenemos la relación:

\displaystyle E^2- p^2 c^2 = - m^2 c^4 (13)
La conclusión de todo esto es clara: si aplicamos a los neutrinos las mismas leyes y relaciones entre energía y momento que aplicamos a los fermiones, obtenemos masas imaginarias o velocidades superluminicas. Es decir, los formalismos fermiónicos aplicados a neutrinos nos ofrecen valores negativos para los cuadrados de sus masas. Pero si aplicamos una relación de dispersión energía-momento distinta, no obtenemos esos valores imaginarios sino valores reales. Los neutrinos, no tienen por que viajar a velocidades superluminicas, simplemente obedecen la relación E²- p²c² = – m²c4. Por el contrario, los leptones, que tampoco tienen por que viajar a velocidades superlumínicas, poseen esta otra relación de dispersión: E²- p²c² = m²c4.
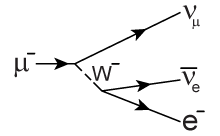
Analicemos brevemente una desintegracion de Michel para un muón: michel-decay
En dicha desintegración, el muón decae hacia un electrón, más un antineutrino electrónico y un muón neutrino. Si desglosamos la dispersión leptónica, obtenemos:

\displaystyle E_\mu^2- p_\mu^2 c^2 = m_\mu^2 c^4 \\ \\ E_e^2- p_e^2 c^2 = m_e^2 c^4 \\ \\ p_{\bar{\nu_e}}^2 c^2 - E_{\bar{\nu_e}}^2 = m_{\bar{\nu_e}}^2 c^4 \\ \\ p_{\nu_\mu}^2 c^2 - E_{\nu_\mu}^2 = m_{\nu_\mu}^2 c^4
esas relaciones ya no nos ofrecen ni velocidades superlumínicas, ni masas imaginarias, ni valores negativos de cuadrados de masas, porque las relaciones de dispersión para los neutrinos que usamos aquí son distintas a las que propone la Relatividad Especial. Si suponemos que esa desintegración del muón se realizó en reposo, entonces las leyes de conservación son:

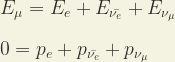\displaystyle E_\mu = E_e+E_{\bar{\nu_e}}+E_{\nu_\mu} \\ \\ 0 = p_e+p_{\bar{\nu_e}}+p_{\nu_\mu} (14)

Donde Eμ = mμc², y pμ = 0, porque el muón se supone en reposo.

Si observamos detenidamente la relación de dispersión entre energía y momento para los neutrinos aquí propuesta, nos daremos cuenta de que si suponemos que un neutrino está en reposo entonces su momento lineal no sería cero, sino:

\displaystyle p = mc\cosh \left(\frac{v}{c}\right) \\ \\ = mc\cosh 0 = mc (15)
Esto implica ni más ni menos que un neutrino en reposo es simplemente una partícula que viaja a la velocidad de la luz, c. ¿Contradicción?. ¿Cómo es posible que una partícula esté moviéndose a una velocidad c si hemos dicho que está en reposo?. En realidad, le pasa lo mismo que a los fotones, lo que ocurre es que los neutrinos sí poseen masa y aún así se mueven a velocidad c. Este fenómeno no puede ser descrito con los formalismos de la Relatividad Especial.

Saludos

This entry was posted on June 10, 2016 at 3:48 pm and is filed under Física de partículas, Matemáticas, Mecánica Cuántica, Relatividad. Tagged: , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

Leave a comment

«
»