TARDÍGRADOS

Ciencia en español -ʟᴀ ʀᴀᴢóɴ ᴇsᴛá ᴀʜí ғᴜᴇʀᴀ-

«
»

La fórmula de Machin para el cálculo acelerado de π

Posted by Albert Zotkin on December 27, 2012

En el año 1706 (ya ha llovido), John Machin nos regaló el primer método de cálculo rápido del número 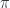\pi, y lo usó para calcularlo hasta una precisión de 100 cifras decimales. Eso fue un logro digno de mención, si consideramos que sus herramientas de cálculo en aquella época eran lápiz y papel. La fórmula de Machin es:

\displaystyle \frac{\pi}{4}= 4\arctan \left (\frac{1}{5} \right ) - \arctan \left (\frac{1}{239} \right )

Obviamente, debe de existir una relación entre los números 1/5 y 1/239. Si indagamos un poquito llegaremos a la conclusión de que para muchos números reales x se cumple que,

\displaystyle \frac{\pi}{4}= 4\arctan\left(\frac{1}{x+\sqrt{1+x^2}+\sqrt{2+2x^2+2 x \sqrt{1+x^2}}}\right ) -\arctan\left(\frac{-1+ x}{-1-x}\right )

Para el caso de la fórmula de Machín resulta más que obvio que ese número real es x=\frac{119}{120}. Podemos jugar a encontrar números reales x tal que (\frac{-1- x}{-1+x}) y (x+\sqrt{1+x^2}+\sqrt{2+2 x^2+2 x \sqrt{1+x^2}}) sean número enteros. Podemos implementar esa tarea (por ejemplo para 10000 iteraciones) en Mathematica así:

Do[x = y /.Solve[y+Sqrt[1+y^2]+Sqrt[2+2y^2+2ySqrt[1+y^2]] == t, y][[1]]; If[IntegerQ[((-1-x)/(-1+x))], Print[x, “, {“, (-1-x)/(-1+x), “, “, t, “}”]], {t, 10000}]

Al ejecutar esa tarea para 100000 iteraciones vemos que solo imprime el caso \frac{119}{120} \text{,\ \{239, 5\}}, por lo que se puede plantear la conjetura: ¿es x=\frac{119}{239} es único valor que da un par de números naturales, en ese caso \{239, 5\}?

Para la iteración t=197 tenemos,

\displaystyle \frac{\pi}{4}= 4\arctan \left (\frac{1}{197} \right ) - \arctan \left (-\frac{368831231}{384121583} \right ) = \\ \\ \\ {} \hspace{0.4cm} = 4\arctan \left (\frac{1}{197} \right ) + \arctan \left (\frac{368831231}{384121583} \right )

o esta otra en t=20091,

\displaystyle \frac{\pi}{4}= 4\arctan \left (\frac{1}{20091} \right ) + \arctan \left (\frac{40724873385497839}{40741092780684799} \right )

Podemos dibujar los puntos {t, x} en el intervalo {1,100}, y unirlos todos con una linea roja

En la siguiente gráfica se ven todos los puntos a una escala más ajustada

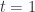Estudiendo un poco estos puntos en la gráfica, vemos que sólo existen cuatro puntos con la coordenada x positiva \{2,\frac{17}{31}\},\{3,\frac{31}{17}\},\{4,\frac{401}{79}\},\{5,239\}, y en particular el punto \{5,239\} constituye un máximo, mientras que el siguiente punto, \{6,-\frac{1921}{241}\} constituye un mínimo. El hipotético punto para t=1 no existe (no está definido). Observamos también que la secuencia de puntos tiende a un límite asintótico en x=-1. 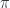Por lo tanto, al ser el punto \{5,239\} el máximo, podemos concluir que la fórmula de Machin constituye la configuración más rápida para el cálculo de \pi respecto a las demás comfiguraciones de pares de números.

Por supuesto, aquí no se acaba la historia de esta fórmulita de Machin. Observamos que de la resta de arcotangentes que dan lugar a \frac{\pi}{4}, la arcotangente minuendo está multiplicada por el factor 4. De hecho la fórmula de Machin corresponde a un desdoblamiento de orden 3 en ese minuendo. Para verlo mejor, debemos partir de la identidad,

\displaystyle \frac{\pi}{4}= \arctan \left (1 \right )

ahora desdoblamos \arctan (1) en una diferencia de dos arcotangentes de forma que \arctan (1) =\arctan (\frac{1}{a})-\arctan (\frac{1}{b})

pero, primero debemos saber cómo restar y sumar arcotangentes. Sabemos que \tan(\alpha+\beta) = (\tan(\alpha)+\tan(\beta))/(1-\tan(\alpha)\tan(\beta)), y por lo tanto \tan(\alpha-\beta) = (\tan(\alpha)-\tan(\beta))/(1+\tan(\alpha)\tan(\beta)). Desde estas dos fórmulas es fácil deducir la suma y resta de arcotangentes, si recordamos que \arctan(\tan(x))=x. Así pues tenemos

\displaystyle \arctan(x) + \arctan(y) = \arctan\left(\frac{x + y}{1 - xy}\right) \\ \\ \\ \arctan(x) - \arctan(y) = \arctan\left(\frac{x - y}{1 + xy}\right)

Una vez que sabemos sumar y restar arcotangentes, podemos continuar con la fórmula de Machin. En el desdoblamiento de orden 1, buscamos dos números, \frac{1}{a} y \frac{1}{b}, tal que

\displaystyle \arctan \left (\frac{1}{a} \right ) - \arctan \left (\frac{1}{b} \right) = \arctan \left (1 \right )

es decir,

\displaystyle \frac{\frac{1}{a}-\frac{1}{b}}{1+\frac{1}{ab}} = 1

con lo cual obtenemos la solución para 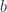b,

\displaystyle b=\frac{-1-a}{-1+a}

y nuestra fórmula de Machin en su primer desdoblamiento de arcotangente quedará así,

\displaystyle \frac{\pi}{4}= \arctan \left (\frac{1}{a} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right )

podemos seguir desdoblando la arcotangente minuendo, dejando invariante la arcotangente sustraendo, con lo cual obtenemos un desdoblamiento de segundo orden. Pero ahora desdoblarenos en una suma en lugar de en una diferencia como antes, con lo cual ahora hay que resolver la ecuación,

\displaystyle \frac{\frac{2}{c}}{1-\frac{1}{c^2}} = \frac{1}{a}

para obtener

\displaystyle c=a\pm\sqrt{1+a^2}

o sea, tenemos dos soluciones igualmente válidas, para el desdoblamiento de segundo orden,

\displaystyle {} \hspace{0.65cm} \frac{\pi}{4}= 2\arctan \left (\frac{1}{a-\sqrt{1+a^2}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right ) \\ \\ \\ \\ -\frac{3\pi}{4}= 2\arctan \left (\frac{1}{a+\sqrt{1+a^2}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right )

si ahora seguimos desdoblando la arcotangente minuendo en suma de dos arcotangentes, obtendremos el desdoblamiento de tercer orden, que corresponde, como he dicho ya, a la fórmula de Machin misma, y para ello hay que resolver la ecuación

\displaystyle \frac{\frac{2}{d}}{1-\frac{1}{d^2}} = \frac{1}{a+\sqrt{1+a^2}}

para la primera solución, y

\displaystyle \frac{\frac{2}{d}}{1-\frac{1}{d^2}} = \frac{1}{a-\sqrt{1+a^2}}

para la segunda solución. Con lo cual obtendremos cuatro soluciones para el desdoblamiento de tercer orden,

\displaystyle {} \hspace{0.65cm} \frac{\pi}{4}=4\arctan \left (\frac{1}{a+\sqrt{1+a^2}+\sqrt{2+2 a^2+2 a \sqrt{1+a^2}}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right ) \\ \\ \\ -\frac{7\pi}{4}= 4\arctan \left (\frac{1}{a+\sqrt{1+a^2}-\sqrt{2+2 a^2+2 a \sqrt{1+a^2}}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right ) \\ \\ \\ \\ -\frac{3\pi}{4}= 4\arctan \left (\frac{1}{a-\sqrt{1+a^2}-\sqrt{2+2 a^2-2 a \sqrt{1+a^2}}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right ) \\ \\ \\ {} \hspace{0.4cm} \frac{5\pi}{4}=4\arctan \left (\frac{1}{a-\sqrt{1+a^2}+\sqrt{2+2 a^2-2 a \sqrt{1+a^2}}} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right )

Intentaré ahora abordar un desdoblamiento de cuarto orden a ver qué encontramos por ahi. Sólo consideraré la primera de las cuatro soluciones. Para ello hay que resolver una ecuación como esta,

\displaystyle \cfrac{\frac{2}{w}}{1-\frac{1}{w^2}} = \cfrac{1}{\frac{1}{a+\sqrt{1+a^2}+\sqrt{2+2 a^2+2 a \sqrt{1+a^2}}} }

y su primera solución es;

\displaystyle w= \frac{1}{2} \left(2 a+2 \sqrt{1+a^2}+2 \sqrt{2} \sqrt{1+a^2+a \sqrt{1+a^2}}+\sqrt{4+\left(2 a+2 \sqrt{1+a^2}+2 \sqrt{2} \sqrt{1+a^2+a \sqrt{1+a^2}}\right)^2}\right)

por lo tanto obtenemos,

\displaystyle {} \hspace{0.65cm}\frac{\pi}{4}=8\arctan \left (\frac{1}{w} \right ) - \arctan \left (\frac{-1+a}{-1-a} \right )

Es engorroso este procedimiento con todas estas expresiones de sumas con raices cuadradas. En realidad lo único que estamos haciendo es aplicar recursivamente la fórmula de la suma o la de la diferencia para hallar los coeficientes del siguiente orden. Es decir, si aplicamos la suma, tenemos

\displaystyle \dfrac{\frac{2}{a_{n+1}}}{1-\frac{1}{a_{n+1}^2}}=\dfrac{1}{a_n}

que tiene dos soluciones,

\displaystyle a_{n+1}=a_n\pm\sqrt{1+a_n^2}

Por lo tanto, una fórmula de Machin de grado n+1 quedaría así,

\displaystyle {} \hspace{0.65cm}\frac{\pi}{4}=(2^n)\arctan \left (\frac{1}{a_n\pm\sqrt{1+a_n^2}} \right ) - \arctan \left (\frac{-1+a_0}{-1-a_0} \right )

Para bifurcar mediante una resta hay que hacerlo con dos coeficientes distintos a_{n+1}\ne b_{n+1}, ya que si fueran iguales, su diferencia siempre sería cero y la bifurcación colapsaría estúpidamente a cero. Así pues tenemos que, por ejemplo, el coeficiente a_{n+1} puede ser cierto porcentaje arbitrario 1/k_n del coeficiente a_n, es decir, k_n a_n = a_{n+1}. Por lo tanto, ahora tenemos,

\displaystyle \dfrac{\frac{1}{k_n a_n}-\frac{1}{b_{n+1}}}{1+\frac{1}{k_n a_n b_{n+1}}} = \dfrac{1}{a_n}

cuya solución es

\displaystyle b_{n+1} = \frac{-1-k_n a_n^2}{(-1+k_n) a_n}

O sea, si queremos bifurcar \arctan(1/a_n) mediante una resta, elegimos al azar un peso k_n, por ejemplo k_n=3, por lo que tendremos,

\displaystyle \arctan \left (\frac{1}{a_n} \right ) = \arctan \left (\frac{1}{k_na_n}\right ) - \arctan \left (\frac{a_n(-1+k_n)}{-1- k_n a_n^2}\right ) \\ \\ \\ \arctan \left (\frac{1}{a_n} \right ) = \arctan \left (\frac{1}{3a_n}\right ) - \arctan \left (\frac{2a_n}{-1-3 a_n^2}\right )

De esta forma tan sencilla, podemos elaborar el árbol genealógico de todas las fórmulas de Machin. Eligiendo el convenio de que una bifurcación (rama) a la izquierda es desdoblamiento mediante resta, y una bifurcación a la derecha es desdoblamiento mediante suma. Las sumas se tratan con sumandos iguales, así, cuando bifurcamos mediante suma, al ser igual los dos sumando, lo único que estamos haciendo es hallando su mitad y multiplicarla por 2,

\displaystyle \arctan \left (\frac{1}{a_n} \right ) = 2\arctan \left (\frac{1}{a_n\pm\sqrt{1+a_n^2}}\right )

Pero, también podemos sumar poniendo más peso en uno de los sumando que en el otro, igual que haciamos con la resta para que no colapsara a cero. De esta forma, eligiendo aleatoriamente un porcentaje k_n, resolvemos la ecuación

\displaystyle \dfrac{\frac{1}{k_n a_n}+\frac{1}{b_{n+1}}}{1-\frac{1}{k_n a_n b_{n+1}}} = \dfrac{1}{a_n}

cuya solución es

\displaystyle b_{n+1} =\frac{1+a_n^2 k_n}{a_n \left(-1+k_n\right)}

y la suma quedaría así,

\displaystyle \arctan \left (\frac{1}{a_n} \right ) = \arctan \left (\frac{1}{k_na_n}\right ) + \arctan \left ( \frac{a_n \left(-1+k_n\right)}{1+a_n^2 k_n} \right )

Todo esto es muy bonito, pero podemos controlar mejor esta clase de fórmulas de Machin, si utilizamos números complejos. Sólo hay que darse cuenta que el argumento (ángulo) del numero complejo (a +ib) es \varphi=\arctan(b/a). O sea, si a=b entonces \varphi=\pi/4=\arctan(1). Cuando multiplicamos dos o más números complejos estamos sumando sus argumentos. 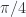Por lo canto, si para el producto de dos números complejos obtenemos otro número complejo cuyas parte real e imaginaria son iguales, (a+ib)(c+id) = k +ik, eso quiere decir el ángulo suma \pi/4, y por lo tanto podemos escribir que \pi/4 = \arctan(b/a) + \arctan(d/c). y si esos números complejos que se multiplican están elevados a los exponentes n y m respectivamente, (a+ib)^n (c+id)^m = k +ik, entonces podemos decir que \pi/4 = n\arctan(b/a) + m\arctan(d/c).

Las fórmulas de Machin son todas las que se pueden escribir así,

\displaystyle \frac{\pi}{4} = \sum_{n}^N k_n \arctan\frac{1}{a_n}

para los número enteros k_n y a_n. Esto significa que, al usar números complejos para tratar con esta clase de fórmulas, vemos que la parte imagaria es siempre la unidad, es decir, son número de la forma z_n= a_n +i

Pongamos por ejemplo, la fórmula hallada por Kikuo Takano en 1982,

\displaystyle \frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}

Esa fórmula obedece al producto de números complejos siguiente:

\displaystyle z=-(49 +i)^{12}(57 +i)^{32}(-239+i)^5(110443+i)^{12}

Al calcular ese producto, vemos que es otro número complejo cuyas parte real e imaginaria son iguales, por eso representa a una fórmula de Machin,

\displaystyle z= 2^{30} 5^{96} 13^{32} 1201^{12} (1+i)

Otro ejemplo, elegimos la fórmula Machin hallada por Gauss

\displaystyle \frac{\pi}{4} = 12 \arctan\frac{1}{18} + 8 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239}

y eso representa el producto de número complejos

\displaystyle z=(18 +i)^{12}(57 +i)^8(-239+i)^5=-2^6 5^{24} 13^{20} (1+i)

La expansión en series de potencias de \arctan y es,

\displaystyle \arctan y = y - \frac {y^3} {3} +\frac {y^5} {5} -\frac {y^7} {7} +\cdots \\ {} \hspace{1.7cm} = \sum_{n=0}^\infty \frac {(-1)^n y^{2n+1}} {2n+1} ; \qquad | y | \le 1 \qquad y \neq i,-i

Para y=1 la serie es,

\displaystyle \arctan 1 = \sum_{n=0}^\infty \frac {(-1)^n } {2n+1}

y esa serie converge muy lentamente hacia 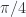\pi/4. El número complejo que representa a esta serie es (1+i). El número complejo que representa a la fórmula de Machin hallada por Gauss, que he escrito arriba, es (18 +i)^{12}(57 +i)^8(-239+i)^5=-2^6 5^{24} 13^{20} (1+i). A simple vista vemos que esta última está formada por la suma de tres arcotangentes, y cada una por separado converge hacia su valor muy rápidamente. En primer lugar tenemos el sumando 12\arctan \frac{1}{18}, y los tres sumandos son

\displaystyle 12\arctan \frac{1}{18} = 12\sum_{n=0}^\infty \frac {(-1)^n} {(2n+1)(18)^{2n+1}} \\ \\ 8\arctan \frac{1}{57} = 8\sum_{n=0}^\infty \frac {(-1)^n } {(2n+1)(57)^{2n+1}} \\ \\ 5\arctan \frac{1}{239} = 5\sum_{n=0}^\infty \frac {(-1)^n} {(2n+1)(239)^{2n+1}}

O sea, para la Machin de Gauss tenemos,

\displaystyle \frac{\pi}{4} = \sum_{n=0}^\infty \frac {(-1)^n} {(2n+1)} \left (\frac{12}{18^{2n+1}} + \frac{8}{57^{2n+1}} - \frac{5}{239^{2n+1}} \right )

La pregunta es ¿nos está informando el coeficiente 2^6 5^{24} 13^{20} de que la serie para la Machin de Gauss converge mucho más rápido que la simple para \arctan 1?

This entry was posted on December 27, 2012 at 10:20 pm and is filed under Matemáticas. Tagged: , , , , , , , , . You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.

Leave a comment

«
»