TARDÍGRADOS

Ciencia en español -ʟᴀ ʀᴀᴢóɴ ᴇsᴛá ᴀʜí ғᴜᴇʀᴀ-

Posts Tagged ‘ecuación de Schrödinger’

El eslabón perdido entre la ecuación de Schrödinger y la gravedad

Posted by Albert Zotkin on May 21, 2013

Hola incondicionales de Tardígrados. Hoy vamos a analizar un aspecto insólito de la mecánica cuántica, y es ese que afirma que la mecánica cuántica no incorpora la interacción gravitatoria, pero si las demás interacciones fundamentales. Y veremos cómo eso es simplemente un producto del desconocimiento, pues en la mecánica cuántica la interacción gravitatoria es el núcleo duro desde el que todas las demás interacciones son posibles. Veremos que, un universo sin gravedad seria un universo sin electromagnetismo, sin interacción débil y sin interacción fuerte.

Empecemos. La ecuación de Schrödinger, que es una de las piezas claves de la mecánica cuántica, es una ecuación diferencial que describe cómo evolucionan los estados cuánticos de algunos sistemas físicos. Dicha ecuación se deriva partiendo de una onda plana, cuya ecuación es

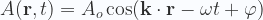\displaystyle A (\mathbf{r}, t ) = A_o \cos (\mathbf{k} \cdot \mathbf{r} - \omega t + \varphi ) (1)
La primera pregunta que hay que hacerse es: ¿Una onda plana de qué?. ¿Qué es lo que vibra?. De momento diré que esas ondas son ondas de materia o también llamadas ondas de De Broglie. Utilicemos ahora la forma compleja de esa función de ondas planas,

\displaystyle \Psi = A_1e^{i(\mathbf{k}\cdot\mathbf{r}-\omega t)} (2)

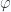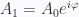donde el desfase \varphi se ha separado como producto en el factor complejo A_1 =A_0e^{i\varphi}.

De las relaciones de De Broglie sabemos que la energía total del sistema está relacionada con la frecuencia angular \omega=2\pi \nu, así,

\displaystyle E = h\nu = \hbar \omega (3)
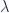
y de igual forma, el momento p es inversamente proporcional a la longitud de onda \lambda , o lo que es lo mismo, directamente proporcional al número de onda k = \frac{2\pi}{\lambda},

\displaystyle p = \frac{h}{\lambda} = \hbar k (4)
Por lo que la ecuación (2) puede ser escrita así,

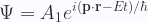\displaystyle \Psi = A_1e^{i(\mathbf{p}\cdot\mathbf{r}-Et)/\hbar} (5)

Si ahora hallamos la derivada parcial de \Psi respecto al espacio, tenemos,

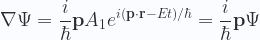\displaystyle \nabla\Psi = \dfrac{i}{\hbar}\mathbf{p}A_1e^{i(\mathbf{p}\cdot\mathbf{r}-Et)/\hbar} = \dfrac{i}{\hbar}\mathbf{p}\Psi (6)

y respecto al tiempo, sería,

\displaystyle \dfrac{\partial \Psi}{\partial t} = -\dfrac{i E}{\hbar} A_1e^{i(\mathbf{p}\cdot\mathbf{r}-Et)/\hbar} = -\dfrac{i E}{\hbar} \Psi (7)
Usemos ahora el inmenso hallazgo que descubrí en mi post anterior (y que nadie parece darse cuenta de su importancia, ya sea por desconocimiento o por reprobación de falsa fé). Este sensacional descubrimiento viene a decir que la energía cinética Ek de una partícula de masa m, que se mueve uniformemente a una velocidad v, es igual al doble del cuadrado del momento lineal q que tendría si se moviera a la mitad de dicha velocidad, dividido por la masa,

\displaystyle E_k =\cfrac{2\ q^2}{m} (8)
Esto, que parece una nimiedad, no es en modo alguno baladí, sino que es la clave para conseguir un avance revolucionario en la mecánica cuántica. Amigos incondicionales de Tardígrados, no encontrareis hasta la fecha ningún libro ni paper de física teórica que nos presente o nos hable de la ecuación (8). Resulta que esa ecuación es relativista, no es clásica, y por lo tanto, al ser usada en la derivación de la ecuación de Schrödinger, lo que obtendremos será es una ecuación relativista.

La energía total de esa partícula de masa m, puede ser ahora expresada así,

\displaystyle E = mc^2+ E_k= mc^2 + 2\cfrac{q^2}{m} (9)

y eso implica que la ecuación en (5) de Schrödinger puede ser transformada en una ecuación relativista así,

\displaystyle \Psi = A_1 \ e^{i(\mathbf{p}\cdot\mathbf{r}-(mc^2 + 2\tfrac{q^2}{m} )t)/\hbar} (10)
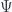
Observamos que la relativista \Psi queda expresada mediante el primer armónico p y el cuadrado del segundo armónico, q2 = q.q. Además. podemos volver a separar la parte constante (desfase), mc2,

\displaystyle \Psi = A_2 \ e^{\frac{i}{\hbar}(\mathbf{p}\cdot\mathbf{r}-2tq^2/m)} (11)

donde obviamente 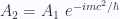A_2= A_1\ e^{-imc^2/\hbar}. Y ahora podemos hallar las derivadas parciales, como en (6) y (7),

\displaystyle \nabla\Psi = \dfrac{i}{\hbar}\mathbf{p}A_2e^{\frac{i}{\hbar}(\mathbf{p}\cdot\mathbf{r}-2tq^2/m)} = \dfrac{i}{\hbar}\mathbf{p}\Psi (12)
\displaystyle \dfrac{\partial \Psi}{\partial t} = -\dfrac{i 2q^2}{\hbar\ m} A_2\ e^{i(\mathbf{p}\cdot\mathbf{r}-2tq^2/m)/\hbar} = -\dfrac{i 2q^2}{\hbar\ m} \Psi (13)

Por otro lado, podemos resumir, recordando que,

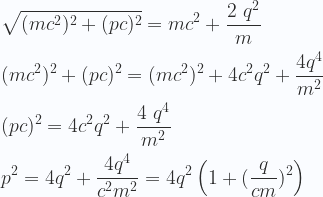\displaystyle \sqrt{(mc^2)^2 + (pc)^2} = mc^2 + \frac{2\ q^2}{m} \\ \\ (mc^2)^2 + (pc)^2 = (mc^2)^2 + 4c^2 q^2 + \frac{4q^4}{m^2} \\ \\ (pc)^2 = 4 c^2 q^2+ \frac{4\ q^4}{m^2} \\ \\ p^2 = 4q^2+ \frac{4q^4}{c^2m^2}= 4q^2 \left (1+ (\frac{q}{cm})^2 \right ) (14)
En cualquier caso, si cuantizamos (9) obtenemos el notable e inmenso resultado (¡ojo!, hasta ahora esto no está en los libros de texto, ni en ningún paper, es cosecha propia mia):

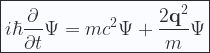\displaystyle \boxed{i \hbar \frac{\partial}{\partial t}\Psi = mc^2\Psi + \frac{2\mathbf{q}^2}{m} \Psi } (15)
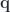
que es una ecuación relativista, ya que entra en juego el momento relativista \mathbf{q}, y siempre sin perder de vista que \mathbf{q} = -i \hbar \mathbf{\nabla} es el operador momento de la partícula cuando tiene una velocidad mitad de la actual, y que es el segundo armónico de la onda plana de De Broglie asociada a dicha partícula. Es decir, por si alguien aún sigue perdido,

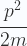\displaystyle \cfrac{p^2}{2m} (16)

es una energía cinética no relativista de una partícula de masa m que se mueve a una velocidad v. Sin embargo,

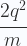\displaystyle \cfrac{2q^2}{m} (17)

es la energía cinética relativista de esa misma partícula cuando se mueve a la misma velocidad v, pero usando el segundo armónico, que corresponde a la mitad de esa velocidad, v/2.

Saludos

Posted in Física de partículas, Gravedad Cuántica, Mecánica Cuántica, Relatividad | Tagged: , , | 4 Comments »