El siguiente artículo es una traducción que he hecho del documento titulado “AT LEAST TWO FIFTHS OF THE ZEROS OF THE RIEMANN ZETA FUNCTION ARE ON THE CRITICAL LINE“, cuyo autor es J. B. CONREY para la AMERICAN MATHEMATICAL SOCIETY. Exactamente el documento original puede encontrarse en BULLETIN (New Series) Volume 20, Number 1, January 1989. Y he añadido dos apéndices de mi cosecha para completar el post.
J. B. CONREY
La función zeta de Riemann, ζ(s), se suele expresar para una variable compleja s = σ + it de la siguiente forma:
 |
En teoría de números es de crucial importancia la distribución de los ceros complejos de la función zeta de Riemann, ζ(s). Todos esos ceros caen dentro del intervalo 0 < σ < 1, y están simétricamente localizados por el eje real y por la línea crítica σ = 1/2. Riemann conjeturó en 1859 que todos esos ceros complejos están en la línea crítica; esa conjetura está aún sin probar, y es conocida como la Hipótesis de Riemann.
El número de ceros de ζ(s) en la región 0 < t < T de la banda crítica se expresa como N(T) y asintóticamente se ofrece así:
 |
cuando T ? ∞. En 1942 Selberg [8] probó que una proporción positiva de los ceros de ζ(s) están en la linea crítica; es decir, si N0(T) es el número de ceros de ζ(s) en el intervalo 0 < t < T que están en la línea crítica, entonces el resultado de Selberg nos dice que
 |
donde κ es la proporción de ceros de ζ(s) que están en la línea crítica. (Fijémonos en que κ = 1 no implica la Hipótesis de Riemann.). Selberg no nos ofreció una cota numérica mínima para κ.
En 1973 Levinson [7] desarrolló un método nuevo y pudo probar que κ > 1/3. Heath-Brown [5] se dió cuenta, e independientemente de Selberg, de que el método de Levinson prueba como cierta la proposición más fuerte de que al menos 1/3 de los ceros de ζ(s) son simples y están en la linea crítica.
Nosotros extendemos el método de Levinson para probar el siguiente teorema:
TEOREMA 1. Al menos 2/5 de los ceros de ζ(s) son simples y están en la línea crítica.
El método de Levinson depende de la abilidad de ofrecer una fórmula asintótica para la media cuadrática en un segmento de linea vertical (a + it : T ≤ t ≤ 2T)) de una combinación lineal de ζ(s) y sus derivadas multiplicadas por un molificador (aproximación a la identidad)
 |
Aquí 
y los coeficientes de molificador se dan con:
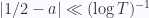
y los coeficientes de molificador se dan con:
 |
donde μ es la función de Möbius y P es un polinomio que satisface P(0) = 0 y P(1) = 1.
En el teorema de Levinson , la longitud y del molificador puede ser tan larga como T 1/2 – ε para un ε > 0 fijo y las apropiadas asíntotas pueden ser deducidas. La principal característica nueva del Teorema 1 es que y = T 4/7 – ε es admisible para cualquier ε > 0. El trabajo de Deshouillers y Iwaniec [4] sobre promedios de sumas de Kloosterman juega un papel crucial aquí. Su trabajo se basa en parte en la fórmula de la traza de Kuznetzov, la cual relaciona sumas de sumas Kloosterman con coeficientes de Fourier de las formas cuspidales de Maass.
Nuestro trabajo también implica dos resultados de densidad para los ceros de ζ(s) que son fuertes cerca de σ = 1/2. Sea N(σ, T) el número de ceros ρ = β + iγ de ζ(s) para los que β ≥ σ y 0 < t ≤ T.
TEOREMA 2. Para cualquier ε > 0 tenemos que
 |
uniformemente para σ ≥ 1/2.
Este teorema mejora el resultado de Jutila [6].
TEOREMA 3. Tenemos
 |
cuando T ? ∞.
Con esto perfeccionamos un poco el resultado de Balasubramanian, Conrey, y Heath-Brown [1].
Los detalles de la prueba del Teorema 1 están en [3].
Referencias
1. R. Balasubramanian, J. B. Conrey, and D. R. Heath-Brown, Asymptotic mean square of the product of the Riemann zeta-function and a Dirichlet polynomial, J.Riene Angew. Math. 357(1985), 161-181. 2. J. B. Conrey, Zeros of derivatives of Riemann’s xi-function on the critical line, J. Number Theory 16(1983), 49-74. 3. , More than two-fifths of the zeros of Riemann’s zeta-function are on the critical line, preprint. 4. J.-M. Deshouillers and H. Iwaniec, Kloosterman sums and Fourier coefficients of cusp forms, Invent. Math. 70 (1982), 219-288. 5. D. R. Heath-Brown, Simple zeros of the Riemann zeta-function on the critical line, Bull. London Math. Soc. 11 (1979), 17-18. 6. M. Jutila, Zeros of the zeta-function near the critical line, Studies in Pure Mathematics, to the memory of Paul Turan, pp. 385-394 (Birkhâuser, Basel Stuttgart, 1982). 7. N. Levinson, More than one-third of the zeros of Riemann’s zeta-function are on o = 1/2, Adv. Math. 13 (1974), 383-436. 8. A. Selberg, On the zeros of Riemann’s zeta-function, Skr. Norskevid. Akad. Oslo 10 (1942), 1-59. 9. E. C. Titchmarsh, The theory of the Riemann zeta-function, (2nd ed.) Clarendon Press,Oxford, 1986.
Apéndice 1 Ceros de la función zeta de Riemann 
Apéndice 2 Ramachandran Balasubramanian es uno de los genios vivos de las matemáticas, aunque no llega a la talla de Ramanujan (nadie llega a la talla de Srinivasa Ramanujan). Nació el 15 de Marzo de 1951, y es el actual director del Instituto de Ciencias Matemáticas en Chennai, India. Es principalmente conocido por sus profundas contribuciones a la Teoría de Números, que incluye la solución al número final g(4) del problema de Waring en 1986. Sus trabajos en momentos de la función zeta de Riemann son muy apreciados, y fue conferenciante plenario por la India en el ICM de 2010. Y fue becario del Institute for Advanced Study en Princeton durante 1980-81.
Conozcamos un poco a este curioso personaje dando una charla en unas jornadas conmemorativas del 50º aniversario de la creación del Instituto de Ciencias Matemáticas en Chennai. https://www.youtube.com/watch?v=8ikdhYCv_Q0
Saludos 🙂
TARDÍGRADOS 